Antisymmetry is a fundamental concept in mathematics and logic, describing a relation where if one element relates to another and vice versa, then the two elements must be identical. This property is crucial in defining partial orders and establishing hierarchies within sets. Explore the full article to understand how antisymmetry shapes structures and influences various fields.
Table of Comparison
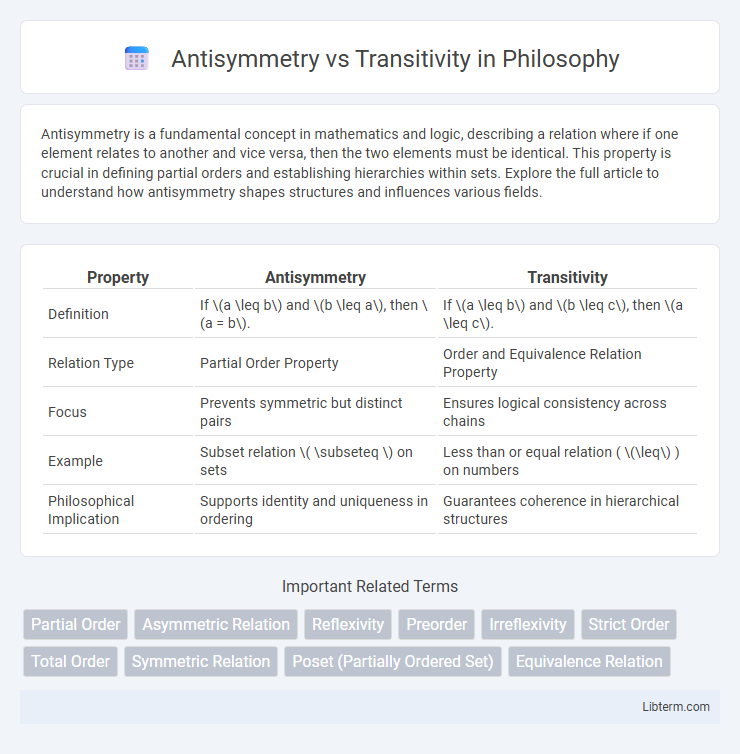
| Property | Antisymmetry | Transitivity |
|---|---|---|
| Definition | If \(a \leq b\) and \(b \leq a\), then \(a = b\). | If \(a \leq b\) and \(b \leq c\), then \(a \leq c\). |
| Relation Type | Partial Order Property | Order and Equivalence Relation Property |
| Focus | Prevents symmetric but distinct pairs | Ensures logical consistency across chains |
| Example | Subset relation \( \subseteq \) on sets | Less than or equal relation ( \(\leq\) ) on numbers |
| Philosophical Implication | Supports identity and uniqueness in ordering | Guarantees coherence in hierarchical structures |
Introduction to Antisymmetry and Transitivity
Antisymmetry is a property of a binary relation where if two elements are mutually related, they must be identical, ensuring no distinct elements relate symmetrically. Transitivity requires that if an element relates to a second, and the second relates to a third, then the first must relate to the third, establishing a chain of relations. These foundational concepts are essential in order theory and graph theory for defining partial orders and equivalence relations.
Defining Antisymmetry in Mathematical Relations
Antisymmetry in mathematical relations is defined such that for a relation \( R \) on a set \( X \), if \( (a, b) \in R \) and \( (b, a) \in R \) imply \( a = b \). This property is crucial in the study of partial orders and distinguishes antisymmetric relations from symmetric ones. Unlike transitivity, which requires that if \( (a, b) \in R \) and \( (b, c) \in R \), then \( (a, c) \in R \), antisymmetry restricts reciprocal pairs to identical elements only.
Understanding Transitivity in Relations
Transitivity in relations refers to the property where if an element a is related to b, and b is related to c, then a must also be related to c. Understanding transitivity is crucial in mathematical structures such as orders and equivalence relations, ensuring consistent linkage among elements. Unlike antisymmetry, which restricts mutual relations between distinct elements, transitivity emphasizes the chainability of relations across multiple elements.
Key Differences Between Antisymmetry and Transitivity
Antisymmetry in relations means that if both (a, b) and (b, a) hold, then a must be equal to b, emphasizing uniqueness in pairs, whereas transitivity requires that if (a, b) and (b, c) hold, then (a, c) must also hold, ensuring a chain of relations. Antisymmetry is primarily concerned with preventing symmetric loops unless elements are identical, contrasting with transitivity's role in extending relational sequences. Key distinctions lie in antisymmetry regulating bidirectional pairs for equality, while transitivity governs the progression of relational links to maintain consistency.
Real-World Examples of Antisymmetric Relations
Antisymmetric relations appear in real-world contexts such as the "subset" relation in set theory, where if set A is a subset of set B and set B is a subset of set A, then A and B are identical, demonstrating antisymmetry. Another example is the "parent" relation in genealogy, where if person A is a parent of person B, and person B is a parent of person A, this situation cannot occur, ensuring antisymmetry. These examples contrast with transitive relations like "ancestor," where if A is an ancestor of B and B is an ancestor of C, then A is an ancestor of C, showing that antisymmetry and transitivity describe different relational properties.
Real-World Examples of Transitive Relations
Transitivity in real-world relations is exemplified by the ancestry relation where if person A is an ancestor of person B, and person B is an ancestor of person C, then person A is an ancestor of person C. Another example is the "less than or equal to" relation among numbers, where if a <= b and b <= c, then a <= c. These transitive relations ensure consistency and allow for hierarchical structuring in databases, genealogy research, and mathematical logic.
Antisymmetry and Transitivity in Set Theory
Antisymmetry in set theory occurs when, for elements a and b in a set, if a is related to b and b is related to a, then a must equal b, often seen in partial orders. Transitivity requires that if a is related to b and b is related to c, then a must be related to c, ensuring a consistent relational structure. These properties are fundamental in defining partial orders, where antisymmetry prevents cycles and transitivity maintains the order's coherence.
Importance in Order Relations and Structures
Antisymmetry and transitivity are fundamental properties in order relations, crucial for defining partial and total orders in mathematical structures. Antisymmetry ensures that if two elements relate mutually, they must be identical, preventing cycles and enabling a well-defined hierarchy. Transitivity guarantees consistent ordering by ensuring that relationships between elements propagate logically, facilitating the construction of ordered sets and lattices essential in algebra and computer science.
Common Misconceptions and Pitfalls
Antisymmetry and transitivity are distinct properties in relation theory often confused due to their overlapping roles in ordering structures. A common misconception is treating antisymmetry as a form of transitivity or vice versa, despite antisymmetry requiring that if two elements relate to each other bidirectionally, they must be identical, while transitivity demands a chain-like consistency in relations. Pitfalls include misapplying antisymmetry conditions to non-partial orders and assuming transitivity guarantees antisymmetry, which can lead to incorrect conclusions about order properties.
Conclusion: Antisymmetry vs Transitivity Summary
Antisymmetry restricts a relation such that if both (a,b) and (b,a) exist, then a must equal b, ensuring no distinct elements relate bidirectionally. Transitivity requires that if (a,b) and (b,c) are present, then (a,c) must also be included, enforcing a chain-like consistency. The fundamental difference lies in antisymmetry limiting reciprocal pairs to identical elements, while transitivity governs the extension of relational pathways.
Antisymmetry Infographic
 libterm.com
libterm.com