Independence empowers individuals to make decisions confidently and pursue personal goals without reliance on others. Cultivating self-reliance enhances your ability to face challenges and achieve success. Discover how embracing independence can transform your life by exploring the rest of this article.
Table of Comparison
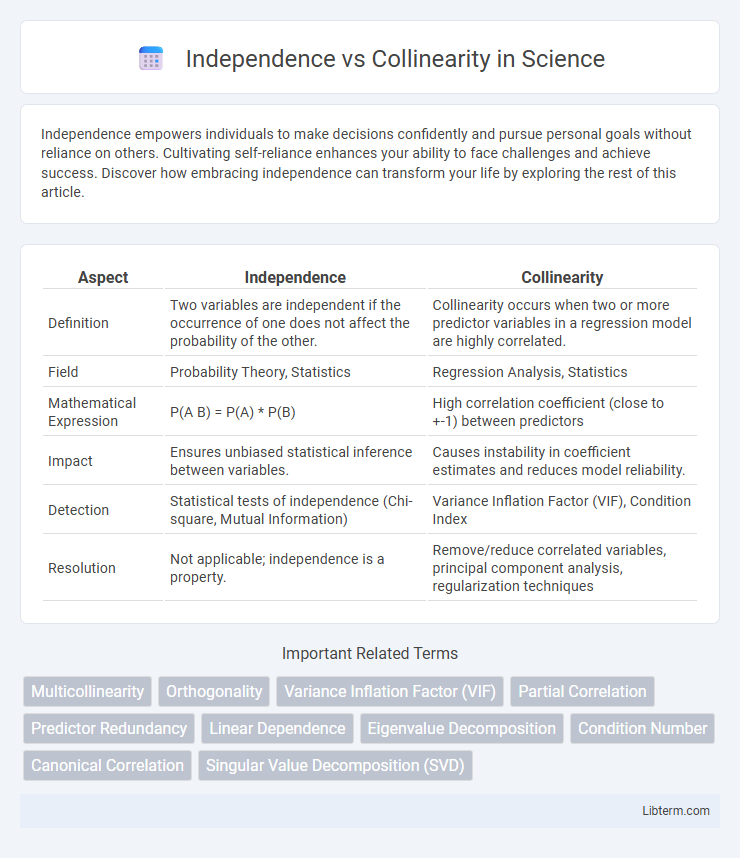
| Aspect | Independence | Collinearity |
|---|---|---|
| Definition | Two variables are independent if the occurrence of one does not affect the probability of the other. | Collinearity occurs when two or more predictor variables in a regression model are highly correlated. |
| Field | Probability Theory, Statistics | Regression Analysis, Statistics |
| Mathematical Expression | P(A B) = P(A) * P(B) | High correlation coefficient (close to +-1) between predictors |
| Impact | Ensures unbiased statistical inference between variables. | Causes instability in coefficient estimates and reduces model reliability. |
| Detection | Statistical tests of independence (Chi-square, Mutual Information) | Variance Inflation Factor (VIF), Condition Index |
| Resolution | Not applicable; independence is a property. | Remove/reduce correlated variables, principal component analysis, regularization techniques |
Understanding Independence in Data Analysis
Independence in data analysis refers to the condition where variables do not influence or predict each other, indicating no statistical relationship. This concept is crucial for ensuring valid model assumptions and accurate inference, as dependent variables can distort results and lead to multicollinearity issues. Understanding independence helps in selecting appropriate features, improving model interpretability, and enhancing the reliability of predictive analytics.
Defining Collinearity and Its Implications
Collinearity occurs when two or more predictor variables in a regression model are highly correlated, causing redundancy in the information they provide. This phenomenon inflates standard errors, undermines the statistical significance of coefficients, and complicates the interpretation of individual predictor effects. Detecting collinearity through metrics like Variance Inflation Factor (VIF) ensures model reliability and facilitates more accurate parameter estimation.
Key Differences: Independence vs Collinearity
Independence refers to the condition where two variables do not influence each other or share any relationship, typically tested through statistical measures like correlation coefficients or mutual information. Collinearity occurs when two or more predictor variables in a regression model exhibit a high degree of linear correlation, leading to redundancy and instability in coefficient estimation. The key difference lies in independence representing no relationship, while collinearity specifically indicates a strong linear relationship between predictors that can distort regression analysis results.
Importance of Independence in Statistical Modeling
Independence in statistical modeling ensures that predictor variables do not provide redundant information, which improves model accuracy and interpretability. Collinearity, or high correlation between predictors, inflates variance estimates of coefficients, leading to unreliable statistical inferences and unstable predictions. Maintaining independence among variables is crucial for robust parameter estimation, reducing multicollinearity issues, and enhancing the model's predictive performance.
Identifying Collinearity Among Predictors
Identifying collinearity among predictors involves examining the correlation matrix and variance inflation factor (VIF) to detect high intercorrelations that can distort regression estimates. Strong collinearity inflates standard errors, undermines coefficient stability, and complicates the interpretation of individual predictor effects. Techniques such as principal component analysis (PCA) or ridge regression help mitigate collinearity by transforming or regularizing correlated variables.
Consequences of Ignoring Collinearity
Ignoring collinearity in regression models leads to inflated standard errors, reducing the statistical power to detect significant predictors. This issue causes unstable coefficient estimates, making it difficult to determine the true relationship between independent variables and the dependent variable. As a result, model interpretation becomes unreliable, potentially misleading decision-making processes and undermining predictive accuracy.
Methods to Test for Independence
Methods to test for independence include the Chi-square test, which evaluates the association between categorical variables by comparing observed and expected frequencies. Another approach is the Pearson correlation coefficient, measuring linear relationships between continuous variables to indicate independence through values near zero. For non-parametric data, Spearman's rank correlation assesses monotonic relationships, with low correlation suggesting independence.
Strategies to Detect and Address Collinearity
Detecting collinearity involves evaluating correlation matrices, variance inflation factors (VIF), and condition indices to identify strongly interrelated predictor variables. Addressing collinearity requires strategies such as removing or combining redundant variables, applying principal component analysis (PCA) for dimensionality reduction, or using regularization techniques like ridge regression to stabilize coefficient estimates. Implementing these approaches improves model interpretability and predictive accuracy by minimizing the adverse effects of multicollinearity in regression analysis.
Real-World Examples: Independence and Collinearity
In statistical modeling, independence occurs when variables have no correlation, such as height and blood type in population studies, while collinearity arises when variables are highly correlated, like income and education level predicting spending habits. Real-world examples highlight that collinearity complicates model interpretation by inflating variance, as seen in economic forecasting where closely related indicators cause unstable coefficient estimates. Independence ensures clearer predictive insights and stable results, essential for accurate risk assessment in finance and clinical research.
Best Practices for Managing Independence and Collinearity
Managing independence and collinearity effectively requires careful variable selection, ensuring predictors contribute unique information to the model. Techniques like variance inflation factor (VIF) analysis help detect multicollinearity, allowing for the removal or combination of highly correlated variables. Centering or standardizing variables and using dimensionality reduction methods such as principal component analysis (PCA) improve model stability and interpretability.
Independence Infographic
 libterm.com
libterm.com