Non-deterministic processes involve outcomes that cannot be precisely predicted, often due to inherent randomness or incomplete information. These systems contrast with deterministic models where each input leads to a specific output, making non-determinism crucial in fields like computer science and decision theory. Explore the full article to understand how non-deterministic concepts influence modern technology and problem-solving.
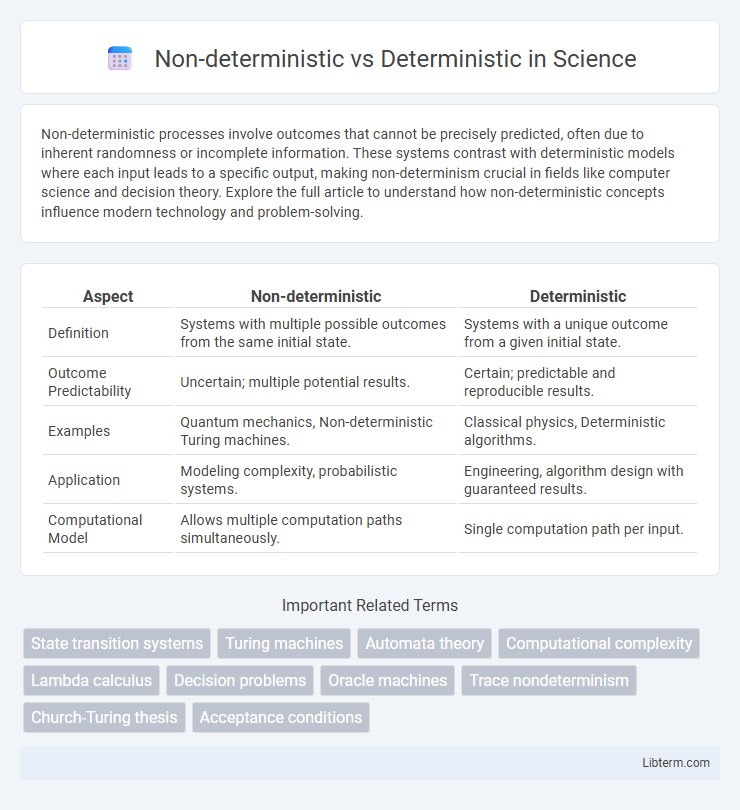
Table of Comparison
| Aspect | Non-deterministic | Deterministic |
|---|---|---|
| Definition | Systems with multiple possible outcomes from the same initial state. | Systems with a unique outcome from a given initial state. |
| Outcome Predictability | Uncertain; multiple potential results. | Certain; predictable and reproducible results. |
| Examples | Quantum mechanics, Non-deterministic Turing machines. | Classical physics, Deterministic algorithms. |
| Application | Modeling complexity, probabilistic systems. | Engineering, algorithm design with guaranteed results. |
| Computational Model | Allows multiple computation paths simultaneously. | Single computation path per input. |
Introduction to Deterministic and Non-deterministic Systems
Deterministic systems operate under fixed rules where a specific input always produces the same output, ensuring predictability and consistency. Non-deterministic systems allow multiple possible outcomes from a single input, introducing variability and uncertainty in behavior. Understanding these fundamental differences is crucial for applications in computer science, automation, and modeling complex real-world processes.
Key Definitions: Deterministic vs. Non-deterministic
Deterministic systems follow a predefined sequence of states or outputs based on given inputs, ensuring predictability and reproducibility in their behavior. Non-deterministic systems, by contrast, allow multiple possible outcomes or state transitions from the same input, introducing unpredictability and enabling exploration of various computation paths simultaneously. Key definitions highlight deterministic models as fixed and unique in response, while non-deterministic models represent systems with branching possibilities that can be leveraged in complexity theory and automata.
Real-world Examples of Deterministic Processes
Deterministic processes in real-world scenarios include clock mechanisms, where each tick follows a fixed sequence, and conveyor belts in manufacturing, which operate with predictable timing and movement. Computer algorithms like sorting routines also exhibit deterministic behavior, executing the same input to produce identical output every time. These processes are characterized by their predictable outcomes without randomness or ambiguity.
Real-world Examples of Non-deterministic Processes
Non-deterministic processes, unlike deterministic ones, exhibit unpredictable outcomes due to inherent randomness or incomplete information, prominently seen in quantum mechanics where particle states cannot be precisely determined until measured. In computer science, non-deterministic algorithms, such as those used in non-deterministic finite automata (NFA), can explore multiple computational paths simultaneously, enabling efficient problem-solving for specific tasks like pattern matching. Real-world non-deterministic processes also appear in weather forecasting, where complex environmental interactions and chaotic dynamics prevent exact predictions despite advanced modeling techniques.
Mathematical Foundations and Theoretical Background
Non-deterministic models, such as Non-deterministic Finite Automata (NFA), allow multiple possible transitions for a given input and state, enabling exploration of various computational paths simultaneously. Deterministic models, like Deterministic Finite Automata (DFA), follow a single computational path with a unique transition for each input symbol from any state. The mathematical foundation of these concepts lies in automata theory and formal languages, where the equivalence of NFAs and DFAs is proved using subset construction, highlighting their theoretical significance in complexity and algorithm design.
Applications in Computer Science and Algorithms
Non-deterministic algorithms enable exploration of multiple computation paths simultaneously, making them essential in solving complex problems like NP-complete issues and optimization tasks. Deterministic algorithms provide predictable outcomes with a single computation path, widely used in sorting, searching, and real-time systems where consistency and repeatability are critical. Applications in computer science leverage non-determinism in fields like quantum computing and automated theorem proving, while deterministic models underpin database transactions and software engineering processes for reliability and efficiency.
Impact on Predictability and Problem Solving
Non-deterministic systems exhibit multiple possible outcomes from the same initial conditions, significantly reducing predictability in problem-solving scenarios compared to deterministic systems where outcomes are fixed and reproducible. This unpredictability in non-deterministic models complicates algorithm design and requires probabilistic or heuristic approaches for solution finding, especially in complex computational problems such as NP-complete class challenges. Deterministic frameworks enable precise simulations and reliable predictions, facilitating more straightforward validation and optimization in engineering, software development, and decision-making processes.
Advantages and Disadvantages of Each Approach
Non-deterministic algorithms offer advantages in solving complex problems faster by exploring multiple potential solutions simultaneously, making them suitable for optimization and search tasks, yet they can lack reproducibility and predictability in results. Deterministic algorithms guarantee consistent and reproducible outputs, facilitating debugging and reliability in critical applications, but may face limitations in efficiency and scalability when addressing problems with vast or uncertain solution spaces. Choosing between non-deterministic and deterministic approaches depends on the trade-off between solution accuracy, computational resources, and the need for predictable behavior in specific use cases.
Implications for Security and Reliability
Deterministic systems guarantee predictable outcomes, enhancing security by reducing vulnerabilities linked to unpredictability, while non-deterministic systems introduce variability that can create challenges in threat detection and risk management. In reliability terms, deterministic processes enable consistent system performance and easier debugging, whereas non-deterministic approaches may increase fault tolerance but complicate replication of issues and recovery procedures. Security frameworks often prefer deterministic models for critical systems to ensure integrity, while non-determinism can be leveraged in cryptographic functions and randomization to strengthen defenses.
Future Trends and Research Directions
Future trends in non-deterministic vs deterministic systems emphasize the development of hybrid computational models that integrate probabilistic reasoning with deterministic algorithms to enhance decision-making under uncertainty. Research is increasingly focused on leveraging quantum computing and advanced machine learning techniques to address scalability and efficiency challenges inherent in non-deterministic processes. Emerging directions prioritize optimizing resource allocation and improving real-time responsiveness, particularly in autonomous systems and complex simulations where predictability and adaptability coexist.
Non-deterministic Infographic
 libterm.com
libterm.com