Classical art emphasizes harmony, balance, and proportion, reflecting the ideals of ancient Greece and Rome. Masterpieces from this period showcase refined techniques and timeless beauty that continue to inspire modern creators. Discover how classical principles influence today's art world by reading the rest of the article.
Table of Comparison
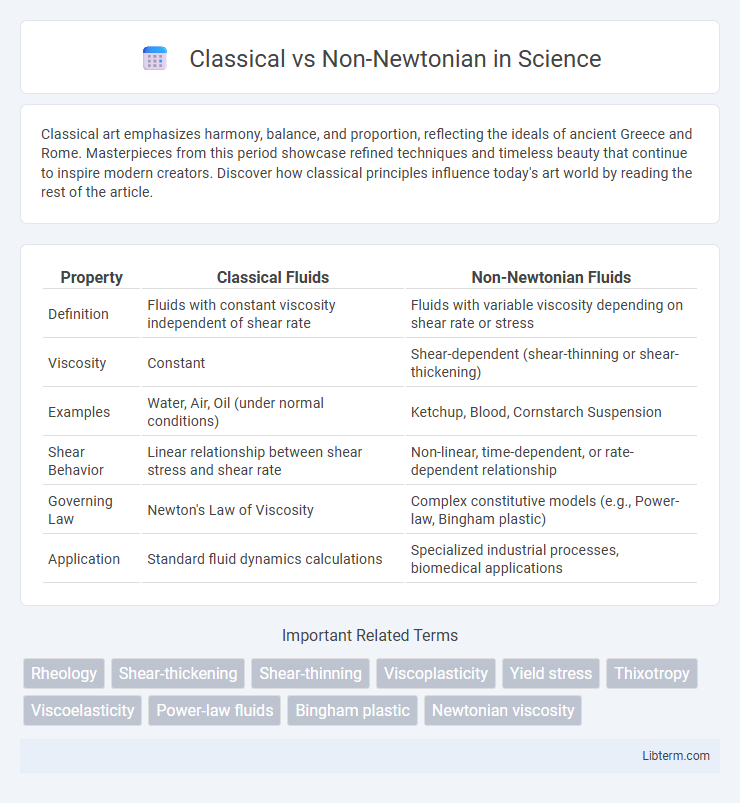
| Property | Classical Fluids | Non-Newtonian Fluids |
|---|---|---|
| Definition | Fluids with constant viscosity independent of shear rate | Fluids with variable viscosity depending on shear rate or stress |
| Viscosity | Constant | Shear-dependent (shear-thinning or shear-thickening) |
| Examples | Water, Air, Oil (under normal conditions) | Ketchup, Blood, Cornstarch Suspension |
| Shear Behavior | Linear relationship between shear stress and shear rate | Non-linear, time-dependent, or rate-dependent relationship |
| Governing Law | Newton's Law of Viscosity | Complex constitutive models (e.g., Power-law, Bingham plastic) |
| Application | Standard fluid dynamics calculations | Specialized industrial processes, biomedical applications |
Introduction to Classical and Non-Newtonian Fluids
Classical fluids, also known as Newtonian fluids, exhibit a constant viscosity regardless of the applied shear rate, meaning their flow behavior follows Newton's law of viscosity with a linear relationship between shear stress and shear rate. Non-Newtonian fluids display variable viscosity, changing in response to shear rate or shear stress, resulting in complex behaviors such as shear thinning, shear thickening, or viscoelasticity. Understanding these fundamental differences is essential for applications in fluid dynamics, material science, and industrial processes involving diverse fluid types.
Defining Fluid Mechanics: Key Concepts
Fluid mechanics studies the behavior of liquids and gases under various forces, differentiating between classical and non-Newtonian fluids based on their flow properties. Classical fluids, or Newtonian fluids, exhibit a constant viscosity regardless of the applied shear rate, exemplified by water and air. Non-Newtonian fluids, including substances like ketchup and blood, display variable viscosity that changes with shear rate, reflecting complex internal structural responses essential for numerous industrial and biomedical applications.
Properties of Classical (Newtonian) Fluids
Classical (Newtonian) fluids exhibit a linear relationship between shear stress and shear rate, characterized by a constant viscosity independent of the applied stress. These fluids, including water, air, and most common liquids, maintain consistent flow behavior under varying conditions. Their predictable viscosity facilitates straightforward calculations in fluid dynamics and engineering applications.
Characteristics of Non-Newtonian Fluids
Non-Newtonian fluids exhibit flow behavior that deviates from Newton's law of viscosity, with viscosity changing based on shear rate or stress. These fluids can display shear-thinning, shear-thickening, thixotropic, or rheopectic properties, meaning their viscosity decreases, increases, or varies over time under constant shear. Examples include ketchup, blood, and oobleck, which demonstrate unique responses such as becoming more liquid or more solid under different flow conditions.
Differences in Flow Behavior
Classical fluids, such as water and air, exhibit a linear relationship between shear stress and strain rate, maintaining a constant viscosity regardless of the applied force. Non-Newtonian fluids, including ketchup and blood, demonstrate variable viscosity that changes with shear rate, resulting in behaviors like shear thinning, shear thickening, or viscoelasticity. These differences in flow behavior critically influence applications in engineering, biomedical fields, and industrial processing.
Common Examples of Newtonian vs. Non-Newtonian Fluids
Water and air represent typical Newtonian fluids, maintaining constant viscosity regardless of applied stress. Ketchup and oobleck exemplify non-Newtonian fluids, whose viscosity changes under varying shear rates or stress. Understanding these fluids' behavior is crucial in fields like materials science, engineering, and food processing.
Mathematical Models and Equations
Classical fluids are modeled by Newton's law of viscosity, where shear stress is proportional to the rate of strain, typically expressed by the linear equation t = m(du/dy), with constant viscosity m. Non-Newtonian fluids require more complex mathematical models such as the power-law equation t = K(du/dy)^n, where K is the consistency index and n the flow behavior index, reflecting shear-thinning or shear-thickening behavior. Models like the Bingham plastic equation t = t0 + m_p(du/dy) incorporate yield stress t0, capturing viscoplastic properties absent in Newtonian fluid descriptions.
Practical Applications and Industries
Classical fluids, characterized by constant viscosity, are widely used in industries such as water treatment, oil pipelines, and chemical manufacturing due to their predictable flow behavior. Non-Newtonian fluids, which exhibit variable viscosity under stress, find practical applications in food processing (e.g., ketchup and sauces), cosmetics, and biomedical sectors where shear-thinning or shear-thickening properties are essential. Understanding the rheological behavior of these fluids enables optimized process control and product formulation across diverse industrial applications.
Experimental Techniques for Fluid Analysis
Classical fluid analysis primarily employs techniques like viscometry and rheometry to measure consistent viscosity and shear stress, providing baseline data for Newtonian fluids. Non-Newtonian fluid analysis requires advanced methods such as rotational rheometers and capillary break-up extensional rheometry (CaBER) to capture shear-thinning, shear-thickening, and viscoelastic behaviors under varying shear rates. High-speed imaging and microfluidic devices are also utilized to analyze complex flow patterns and transient responses unique to non-Newtonian fluids.
Future Trends in Fluid Dynamics Research
Future trends in fluid dynamics research emphasize advanced modeling of classical Newtonian fluids alongside complex non-Newtonian behaviors, driven by innovations in machine learning and high-performance computing. Emerging studies prioritize real-time simulations and multiscale approaches to better predict flow characteristics in biomedical, industrial, and environmental applications. Integration of smart materials and adaptive control systems is expected to revolutionize the manipulation and optimization of fluid properties in diverse engineering fields.
Classical Infographic
 libterm.com
libterm.com