Relativistic effects become significant when objects move at speeds close to the speed of light, causing time dilation, length contraction, and variations in mass. These phenomena challenge classical mechanics and are crucial for understanding high-energy physics and cosmology. Explore the article to uncover how relativistic principles impact your perception of space and time.
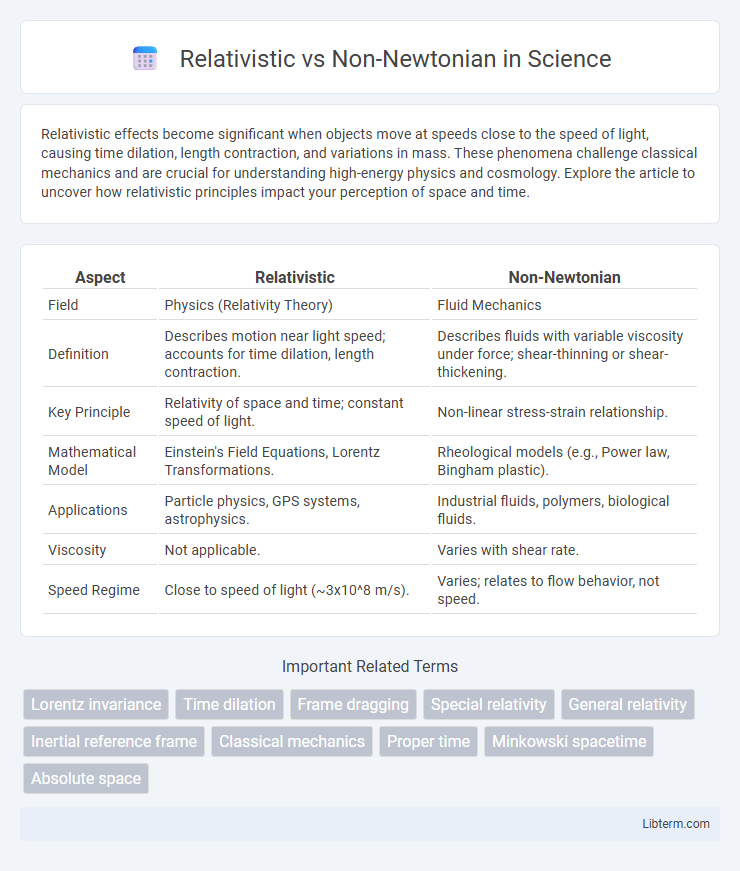
Table of Comparison
| Aspect | Relativistic | Non-Newtonian |
|---|---|---|
| Field | Physics (Relativity Theory) | Fluid Mechanics |
| Definition | Describes motion near light speed; accounts for time dilation, length contraction. | Describes fluids with variable viscosity under force; shear-thinning or shear-thickening. |
| Key Principle | Relativity of space and time; constant speed of light. | Non-linear stress-strain relationship. |
| Mathematical Model | Einstein's Field Equations, Lorentz Transformations. | Rheological models (e.g., Power law, Bingham plastic). |
| Applications | Particle physics, GPS systems, astrophysics. | Industrial fluids, polymers, biological fluids. |
| Viscosity | Not applicable. | Varies with shear rate. |
| Speed Regime | Close to speed of light (~3x10^8 m/s). | Varies; relates to flow behavior, not speed. |
Understanding Relativistic Physics
Relativistic physics explores phenomena occurring at velocities approaching the speed of light, where time dilation, length contraction, and mass-energy equivalence become significant. Unlike non-Newtonian mechanics, which assumes absolute time and space, relativistic physics relies on Einstein's theory of special relativity to accurately describe high-speed particle behavior and electromagnetic interactions. Grasping relativistic concepts is essential for advancements in astrophysics, particle accelerators, and GPS technology, where precise calculations of motion and time are critical.
Key Principles of Non-Newtonian Mechanics
Non-Newtonian mechanics examines materials whose viscosity changes under stress or strain, deviating from classical Newtonian fluid behavior with constant viscosity. Key principles include time-dependent viscosity, shear-thinning and shear-thickening behaviors, and viscoelasticity, where materials exhibit both fluid and solid characteristics depending on applied forces. These principles enable the analysis of complex fluids like polymers, gels, and suspensions, essential for industries ranging from biomedical engineering to food processing.
Fundamental Differences: Relativistic vs Non-Newtonian
Relativistic physics deals with objects moving at speeds close to the speed of light, where the effects of special relativity, such as time dilation and length contraction, become significant, fundamentally altering classical Newtonian mechanics. Non-Newtonian fluids, on the other hand, exhibit complex flow behaviors that deviate from Newton's law of viscosity, with their viscosity changing under stress or strain, unlike relativistic phenomena which concern the nature of space-time and mass-energy equivalence. The key distinction lies in relativistic physics addressing high-velocity dynamics governed by Einstein's theory, whereas non-Newtonian fluid mechanics focuses on the variable flow properties of materials under applied forces.
Historical Development and Milestones
Relativistic physics emerged in the early 20th century with Albert Einstein's theory of special relativity in 1905, revolutionizing concepts of space, time, and gravity beyond Newtonian mechanics established in the 17th century by Isaac Newton. Key milestones include the confirmation of time dilation through the Hafele-Keating experiment in 1971 and the prediction of gravitational waves, directly detected by LIGO in 2015, highlighting deviations from classical Newtonian invariance. Non-Newtonian mechanics primarily evolved through advancements in fluid dynamics and material science during the 20th century, focusing on complex fluids exhibiting shear-dependent viscosity, with important developments such as the recognition of pseudoplastic and dilatant behavior in polymers and suspensions enabling applications in biomedicine and industrial processes.
Equations and Mathematical Foundations
Relativistic mechanics relies on the Lorentz transformation equations and the energy-momentum relation \( E^2 = (pc)^2 + (m_0c^2)^2 \), extending classical mechanics to account for objects moving at speeds comparable to the speed of light, where time dilation and length contraction occur. Non-Newtonian fluid mechanics, governed by nonlinear constitutive equations such as the power-law model \( \tau = K \dot{\gamma}^n \), modifies Newton's law of viscosity to describe fluids with variable viscosity depending on shear rate. The mathematical foundations of relativistic physics extend from Einstein's special relativity postulates and Minkowski spacetime geometry, while Non-Newtonian fluid dynamics are rooted in continuum mechanics and empirical models capturing complex flow behaviors.
Practical Applications in Modern Science
Relativistic physics plays a crucial role in GPS satellite technology by accounting for time dilation effects resulting from high velocities and gravitational fields, ensuring accurate positioning data. Non-Newtonian fluid dynamics are essential in industrial processes such as polymer manufacturing, where materials exhibit shear-thinning or shear-thickening behaviors critical for product consistency and performance. Understanding both relativistic and non-Newtonian principles enables advancements in astrophysics simulations and innovative materials engineering, driving progress across multiple scientific disciplines.
Experimental Evidence and Observations
Experimental evidence for relativistic effects includes precise measurements of time dilation using atomic clocks on fast-moving spacecraft and the deflection of light observed during solar eclipses, confirming predictions of Einstein's theory of relativity. Non-Newtonian fluids demonstrate observable behaviors such as shear-thickening and shear-thinning under various stress conditions, with experiments highlighting viscosity changes in materials like cornstarch suspensions or oobleck. Laboratory observations clearly delineate relativistic phenomena at velocities approaching light speed, whereas non-Newtonian fluid behavior is characterized by complex, rate-dependent viscosity in everyday materials.
Common Misconceptions and Clarifications
Relativistic physics involves objects moving at speeds close to the speed of light, where time dilation and mass increase occur, while non-Newtonian fluids change viscosity under stress and do not relate to relativistic effects. A common misconception is confusing non-Newtonian behavior with relativistic phenomena, despite their fundamentally different physical principles. Clarifying these differences is essential for accurate understanding in fields like fluid dynamics and high-energy physics.
Impact on Technology and Industry
Relativistic physics drives advancements in high-speed computing, GPS systems, and particle accelerators by accounting for time dilation and mass-energy equivalence, essential for precision and performance. Non-Newtonian fluid dynamics revolutionize industries like automotive, cosmetics, and food processing through materials whose viscosity changes under stress, enabling innovative product designs and safety features. Understanding both physical frameworks enhances technology development by providing tailored solutions for speed-sensitive applications and adaptive material behaviors.
Future Prospects and Research Directions
Future research in relativistic fluid dynamics emphasizes enhanced computational models to simulate extreme astrophysical environments, such as neutron stars and black hole accretion disks, where relativistic effects dominate. Non-Newtonian fluid studies increasingly target smart materials and biomedical applications, exploring adaptive viscosity and shear-responsive behavior for advanced drug delivery systems and soft robotics. Integrating relativistic frameworks with non-Newtonian rheology could pioneer novel insights into high-energy plasma flows and exotic states of matter, expanding the frontier of theoretical and applied physics.
Relativistic Infographic
 libterm.com
libterm.com