Orthogonal concepts are fundamental in mathematics and computer science, describing elements that are independent or non-overlapping, such as perpendicular vectors or unrelated variables. Understanding orthogonality improves clarity in data analysis, programming, and design by reducing redundancy and enhancing modularity. Explore the rest of the article to deepen your grasp of how orthogonality impacts various fields and your practical applications.
Table of Comparison
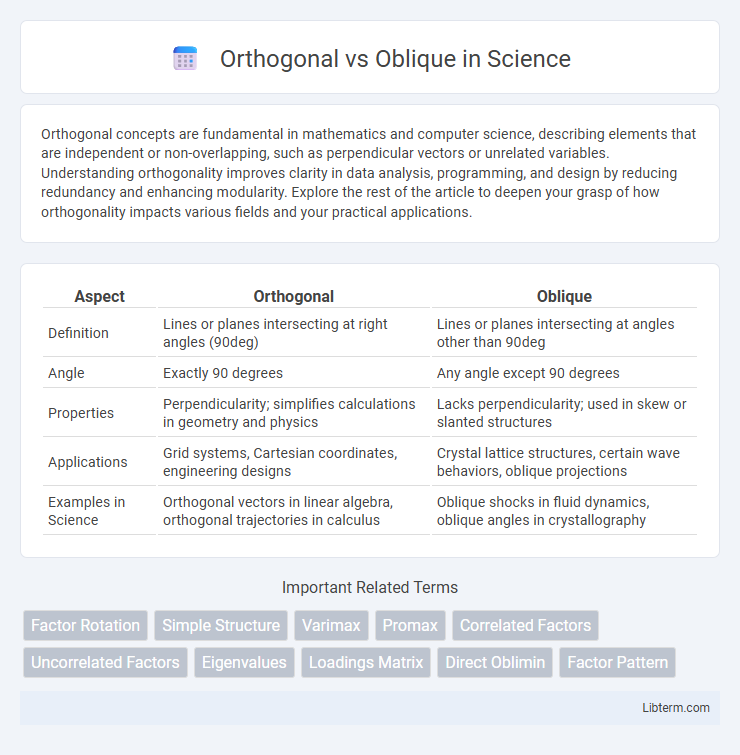
| Aspect | Orthogonal | Oblique |
|---|---|---|
| Definition | Lines or planes intersecting at right angles (90deg) | Lines or planes intersecting at angles other than 90deg |
| Angle | Exactly 90 degrees | Any angle except 90 degrees |
| Properties | Perpendicularity; simplifies calculations in geometry and physics | Lacks perpendicularity; used in skew or slanted structures |
| Applications | Grid systems, Cartesian coordinates, engineering designs | Crystal lattice structures, certain wave behaviors, oblique projections |
| Examples in Science | Orthogonal vectors in linear algebra, orthogonal trajectories in calculus | Oblique shocks in fluid dynamics, oblique angles in crystallography |
Introduction to Orthogonal and Oblique Concepts
Orthogonal concepts refer to elements that are independent and uncorrelated, often represented by axes at right angles in multidimensional space, ensuring no overlap in information or influence. Oblique concepts involve relationships where elements are interdependent or correlated, reflected by axes that intersect at angles other than 90 degrees, capturing more complex interactions. Understanding orthogonal versus oblique distinctions is essential in fields like statistics, signal processing, and design for accurately modeling data structures and system behaviors.
Defining Orthogonal: Meaning and Applications
Orthogonal refers to elements positioned at right angles (90 degrees) to each other, commonly applied in mathematics, computer science, and design to ensure independence or lack of correlation between components. In linear algebra, orthogonal vectors have a dot product of zero, indicating no projection onto each other, which is crucial for simplifying computations and enhancing numerical stability. In design and architecture, orthogonal layouts promote clarity and organization by aligning elements along perpendicular axes, facilitating efficient space utilization and visual coherence.
Understanding Oblique: Key Characteristics
Oblique projections display objects with one face parallel to the viewing plane, causing depth lines to recede at an angle, often 45 degrees, to reveal three-dimensional form. This projection type distorts true scale along the receding axis but allows clearer visualization of the object's shape and features. Common oblique methods like cavalier and cabinet differ in depth scaling, with cavalier maintaining full scale and cabinet halving it for more realistic representation.
Orthogonal vs. Oblique: Core Differences
Orthogonal and oblique are two types of projections used in technical drawing and computer graphics, distinguished primarily by their angle relationships. Orthogonal projection features perpendicular lines between the projection plane and the viewing direction, ensuring accurate scale and shape representation without distortion. Oblique projection, however, involves projecting images at an angle other than 90 degrees, resulting in a distorted but visually informative representation that emphasizes depth.
Mathematical Foundations Explained
Orthogonal vectors in mathematics are characterized by a zero dot product, indicating perpendicularity and independence in Euclidean space, while oblique vectors form an angle other than 90 degrees, implying linear dependence or correlation. The orthogonality condition simplifies computations in vector spaces, particularly in projections and orthogonal decompositions, whereas oblique vectors require more complex transformations and cannot leverage the Pythagorean theorem. Understanding these geometric and algebraic distinctions underpins the design of algorithms in linear algebra, signal processing, and data analysis.
Visualizing Orthogonal and Oblique Relationships
Visualizing orthogonal relationships highlights variables or dimensions that are statistically independent, represented by right angles in scatterplots or correlation matrices, ensuring clear separation of effects. Oblique relationships indicate correlated variables with angles less than 90 degrees, revealing overlapping or interacting factors in dimensionality reduction techniques like factor analysis. Effective visualization distinguishes these patterns, aiding interpretation of complex datasets by clarifying the degree of variable interdependence.
Applications in Data Analysis and Statistics
Orthogonal and oblique rotations play critical roles in factor analysis and principal component analysis to interpret data structures effectively. Orthogonal rotations maintain uncorrelated factors simplifying interpretation by preserving right angles between vectors, commonly employed in techniques like Varimax for clearer factor loadings. Oblique rotations allow factors to correlate, enhancing model fit and revealing more realistic, complex relationships in multivariate datasets, often utilized in Promax or Oblimin methods for nuanced behavioral or social science data analysis.
Benefits and Limitations of Orthogonal Methods
Orthogonal methods offer clear benefits such as simplified interpretation, reduced multicollinearity, and enhanced computational efficiency due to uncorrelated axes in data analysis. These methods facilitate accurate decomposition of variance but can be limited by their rigidity, sometimes failing to capture relationships in data where factors are inherently correlated. The inability to model oblique (non-orthogonal) relationships may reduce their effectiveness in complex real-world datasets requiring flexible factor structures.
When to Use Oblique Approaches
Oblique approaches are preferred when obstacles or terrain prevent a direct orthogonal path, allowing for safer and more efficient navigation around barriers. They optimize entry angles, reducing the risk of collision in aviation and enhancing structural stability in engineering designs where orthogonal alignment is unfeasible. Employing oblique angles increases flexibility in spatial planning and accommodates complex environments.
Conclusion: Choosing the Right Technique
Orthogonal designs ensure independent, uncorrelated factor analysis, ideal for experiments requiring clear interpretation and minimal confounding. Oblique techniques allow correlated factors, providing more realistic modeling of complex, interdependent data structures in social sciences or psychology. Selecting the right method depends on research goals: use orthogonal for clarity and simplicity, oblique for capturing nuanced, real-world relationships.
Orthogonal Infographic
 libterm.com
libterm.com