Perpendicular lines intersect at a 90-degree angle, creating precise right angles essential in geometry and construction. Understanding how to identify and work with perpendicular lines enhances accuracy in design and problem-solving. Explore the rest of the article to deepen your grasp of perpendicularity and its practical applications.
Table of Comparison
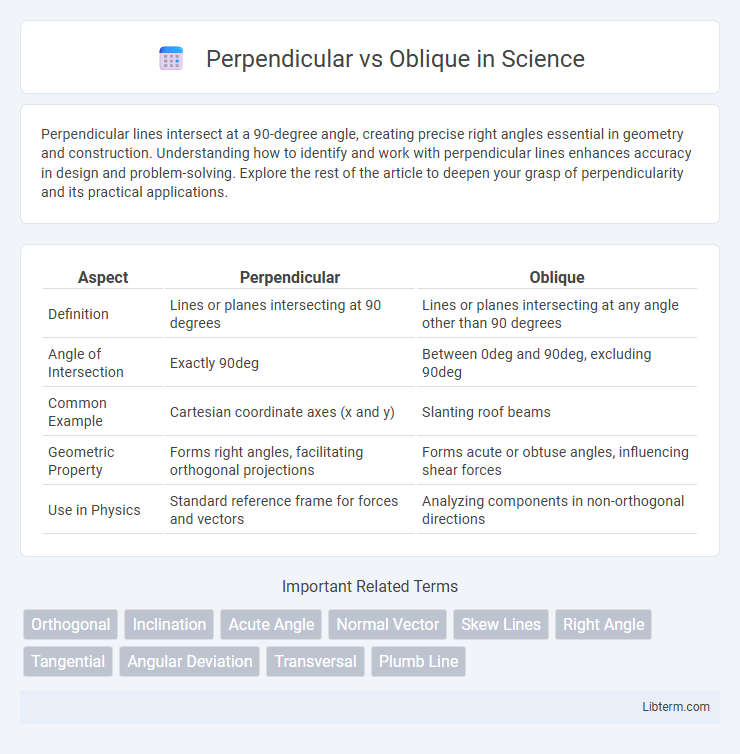
| Aspect | Perpendicular | Oblique |
|---|---|---|
| Definition | Lines or planes intersecting at 90 degrees | Lines or planes intersecting at any angle other than 90 degrees |
| Angle of Intersection | Exactly 90deg | Between 0deg and 90deg, excluding 90deg |
| Common Example | Cartesian coordinate axes (x and y) | Slanting roof beams |
| Geometric Property | Forms right angles, facilitating orthogonal projections | Forms acute or obtuse angles, influencing shear forces |
| Use in Physics | Standard reference frame for forces and vectors | Analyzing components in non-orthogonal directions |
Understanding Perpendicular and Oblique: Definitions
Perpendicular lines intersect at a 90-degree angle, creating right angles and forming the basis for many geometric constructions. Oblique lines intersect at any angle other than 90 degrees, resulting in non-right angles that characterize various shapes and patterns. Understanding the distinction between perpendicular and oblique lines is crucial for applications in geometry, engineering, and design.
Mathematical Distinction: Key Differences
Perpendicular lines intersect at a 90-degree angle, creating right angles that are fundamental in geometry and coordinate systems. Oblique lines intersect at any angle other than 90 degrees, lacking the orthogonal property that defines perpendicularity. This distinction affects calculations in vector spaces, trigonometry, and analytical geometry, where angle measures determine line relationships and function behaviors.
Visualizing Perpendicular vs Oblique Lines
Perpendicular lines intersect at a 90-degree angle, forming four right angles, while oblique lines intersect at any angle other than 90 degrees, creating non-right angles. Visualizing perpendicular lines often involves grids or coordinate planes where the lines meet orthogonally, making it easy to identify right angles. Oblique lines can be recognized by their slanted intersection, requiring angle measurement tools or vector analysis for precise differentiation.
Common Examples in Geometry
Lines that intersect at right angles, such as the perpendicular bisectors of a triangle or the x and y axes on a Cartesian plane, are classic examples of perpendicular lines in geometry. Oblique lines, in contrast, intersect at any angle other than 90 degrees, as seen in the diagonals of parallelograms or the slant edges of a rhombus. Understanding the difference helps identify shapes and their properties, such as right angles in rectangles versus the tilted angles in parallelograms.
Applications in Real-World Design
Perpendicular angles are fundamental in architectural design for creating stable structures, ensuring walls meet floors at 90 degrees for maximum support and safety. Oblique angles are widely used in modern art installations and ergonomic product designs to enhance visual dynamics and user comfort by introducing unconventional, slanted surfaces. Engineering applications leverage both perpendicular and oblique angles to optimize stress distribution in bridges, mechanical joints, and aerospace components.
Impact on Structural Engineering
Perpendicular loads apply force at a 90-degree angle, maximizing structural stability by evenly distributing stress and minimizing bending moments. Oblique loads introduce angled forces that create a combination of bending, shear, and axial stresses, complicating structural analysis and requiring more robust reinforcement. Understanding the impact of load direction is crucial for designing safe and efficient frameworks, especially in bridges, buildings, and other load-bearing structures.
Perpendicular vs Oblique in Coordinate Systems
Perpendicular lines in coordinate systems intersect at right angles, forming 90-degree angles that are fundamental in defining orthogonal axes and simplifying vector calculations. Oblique lines, on the other hand, intersect at angles other than 90 degrees, leading to non-orthogonal coordinate systems that can complicate distance and angle measurements. Understanding the distinction between perpendicular and oblique orientations is crucial for accurate spatial analysis, coordinate transformations, and geometric modeling.
Importance in Physics and Mechanics
Perpendicular and oblique angles play crucial roles in physics and mechanics, defining force directions and motion trajectories. Perpendicular forces often result in maximum work efficiency and equilibrium states, while oblique forces introduce components that affect acceleration and torque. Understanding these angles is essential for analyzing structural stability, calculating vector components, and optimizing mechanical system designs.
Challenges in Calculating Angles
Calculating angles in perpendicular versus oblique scenarios presents distinct challenges; perpendicular angles are fixed at 90 degrees, simplifying measurement but requiring precise verification to avoid errors in construction or design. Oblique angles, which deviate from 90 degrees, demand more complex calculations often involving trigonometric functions such as sine, cosine, and tangent to accurately determine angle size. Errors in measuring oblique angles can lead to significant mistakes in engineering, architecture, and physics due to the angles' dependence on accurate geometric and algebraic computation.
Choosing Between Perpendicular and Oblique Approaches
Choosing between perpendicular and oblique approaches depends on the specific context and desired outcomes in design or construction. Perpendicular approaches offer precise alignment and easier measurement, ideal for creating strong, stable structures or clear geometrical layouts. Oblique approaches provide flexibility and adaptability, useful for complex angles and spatial arrangements where traditional right angles are not feasible.
Perpendicular Infographic
 libterm.com
libterm.com