Chaotic environments often lead to confusion and decreased productivity, making it difficult to focus on essential tasks. Understanding the causes and learning effective strategies to manage chaos can significantly improve your personal and professional life. Explore this article to discover practical tips for bringing order to chaos and enhancing your well-being.
Table of Comparison
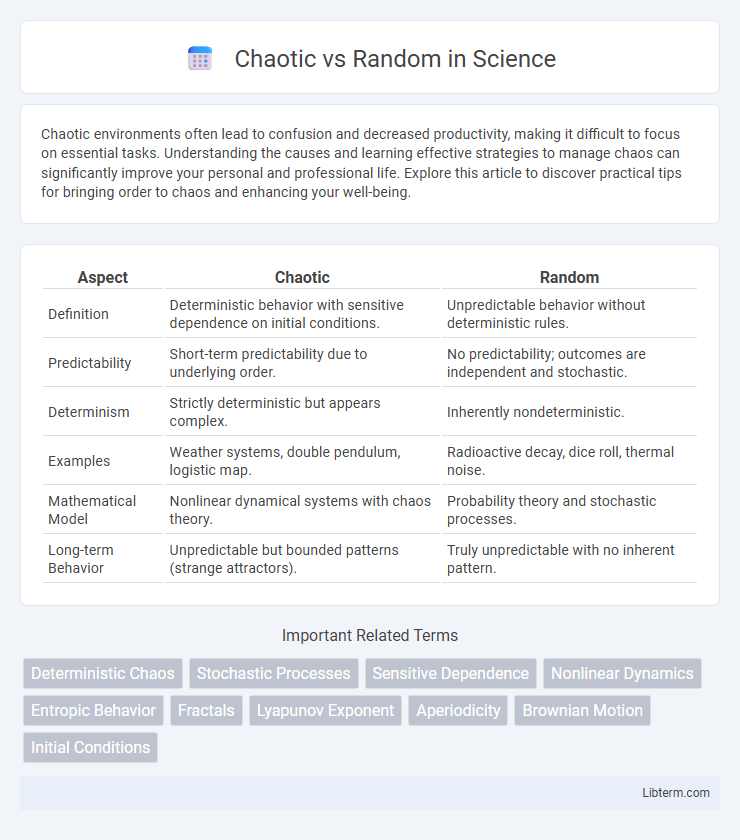
| Aspect | Chaotic | Random |
|---|---|---|
| Definition | Deterministic behavior with sensitive dependence on initial conditions. | Unpredictable behavior without deterministic rules. |
| Predictability | Short-term predictability due to underlying order. | No predictability; outcomes are independent and stochastic. |
| Determinism | Strictly deterministic but appears complex. | Inherently nondeterministic. |
| Examples | Weather systems, double pendulum, logistic map. | Radioactive decay, dice roll, thermal noise. |
| Mathematical Model | Nonlinear dynamical systems with chaos theory. | Probability theory and stochastic processes. |
| Long-term Behavior | Unpredictable but bounded patterns (strange attractors). | Truly unpredictable with no inherent pattern. |
Understanding Chaos and Randomness
Chaos refers to deterministic systems highly sensitive to initial conditions, where small differences lead to vastly different outcomes, making long-term prediction difficult despite an underlying order. Randomness implies complete unpredictability with no deterministic cause, often modeled by stochastic processes or probability distributions. Understanding chaos involves analyzing nonlinear dynamics and attractors, while randomness is studied through statistical methods and probability theory.
Defining Chaotic Systems
Chaotic systems are deterministic processes characterized by extreme sensitivity to initial conditions, leading to seemingly unpredictable behavior despite underlying order. These systems exhibit nonlinearity and dynamic complexity, where small changes can cause vastly different outcomes. Unlike random systems driven by inherent randomness, chaotic systems follow precise mathematical rules but generate patterns that appear erratic and complex.
What Constitutes Randomness?
Randomness constitutes outcomes generated without predictable patterns or deterministic rules, often characterized by statistical independence and uniform probability distributions. In contrast, chaotic systems exhibit deterministic behavior governed by nonlinear equations, producing seemingly unpredictable results due to extreme sensitivity to initial conditions. The core difference lies in randomness lacking underlying order, whereas chaos involves hidden structure within apparent disorder.
Key Differences Between Chaotic and Random Behavior
Chaotic behavior arises from deterministic systems that are highly sensitive to initial conditions, producing complex but predictable patterns over time, whereas random behavior lacks any deterministic rules and is inherently unpredictable. Chaotic systems exhibit underlying order and structure, identifiable through attributes such as strange attractors and fractal dimensions, contrasting with the completely stochastic nature of random processes. Understanding these differences is crucial in fields like physics and finance, where chaotic models can predict system dynamics better than purely random models.
Mathematical Foundations of Chaos and Randomness
Chaotic systems are governed by deterministic nonlinear equations that exhibit extreme sensitivity to initial conditions, leading to complex and seemingly unpredictable behavior despite underlying order. Randomness is characterized by stochastic processes with outcomes that cannot be precisely predicted, often modeled using probability theory. The mathematical foundations of chaos involve concepts such as Lyapunov exponents and strange attractors, whereas randomness relies on measure theory and probabilistic independence.
Real-World Examples of Chaotic Systems
Chaotic systems such as weather patterns, double pendulums, and population dynamics exhibit sensitive dependence on initial conditions, making long-term prediction inherently difficult despite deterministic rules. Real-world examples include atmospheric turbulence where small changes can lead to vastly different weather outcomes and financial markets where intricate feedback loops produce complex price fluctuations. These systems contrast with random processes by having underlying order governed by nonlinear differential equations rather than pure stochasticity.
Real-World Examples of Random Processes
Random processes appear in various real-world phenomena such as radioactive decay, where particles emit unpredictably with a constant probability over time, and in financial markets, where stock price movements follow stochastic models reflecting inherent unpredictability. Weather fluctuations also demonstrate randomness through complex interactions among atmospheric variables, producing outcomes that resist precise prediction despite underlying physical laws. These examples highlight how random processes generate unpredictable patterns fundamentally different from deterministic chaotic systems governed by specific initial conditions.
Predictability in Chaos vs. Randomness
Chaos theory describes systems that appear random but are fundamentally deterministic, allowing for short-term predictability despite long-term unpredictability due to sensitive dependence on initial conditions. Randomness involves true unpredictability, where outcomes follow no deterministic pattern and cannot be forecasted even in the short term. In chaotic systems, precise knowledge of initial states enables limited prediction, whereas purely random processes lack such a foundation for prediction altogether.
Applications in Science and Technology
Chaotic systems exhibit deterministic behavior with sensitive dependence on initial conditions, making them essential for secure communication protocols and weather prediction models. Random processes, characterized by inherent unpredictability, underpin probabilistic algorithms in quantum computing and stochastic simulations. Both phenomena influence advancements in cryptography, signal processing, and artificial intelligence by providing distinct frameworks for handling uncertainty and complexity.
Implications for Future Research and Understanding
Distinguishing chaotic systems from random processes holds significant implications for future research, particularly in fields such as meteorology, finance, and neuroscience, where predicting complex behaviors is crucial. Improved methods to identify deterministic chaos could enhance model accuracy and lead to more reliable forecasts, enabling deeper insights into underlying mechanisms. Emphasizing the nuanced differences between chaos and randomness will drive advancements in algorithms and theoretical frameworks, ultimately refining our understanding of complex dynamical systems.
Chaotic Infographic
 libterm.com
libterm.com