Field work offers hands-on experience and a direct connection to natural environments, enhancing practical skills and observational abilities. Understanding the dynamics of various fields is crucial for applying theoretical knowledge effectively and solving real-world problems. Explore the rest of the article to discover how field expertise can transform your approach and boost your career.
Table of Comparison
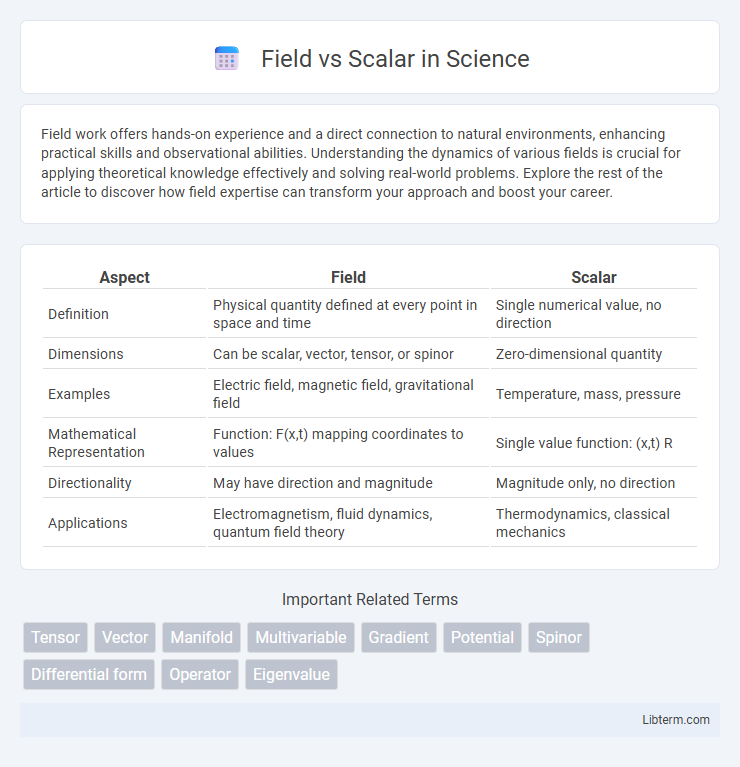
| Aspect | Field | Scalar |
|---|---|---|
| Definition | Physical quantity defined at every point in space and time | Single numerical value, no direction |
| Dimensions | Can be scalar, vector, tensor, or spinor | Zero-dimensional quantity |
| Examples | Electric field, magnetic field, gravitational field | Temperature, mass, pressure |
| Mathematical Representation | Function: F(x,t) mapping coordinates to values | Single value function: (x,t) R |
| Directionality | May have direction and magnitude | Magnitude only, no direction |
| Applications | Electromagnetism, fluid dynamics, quantum field theory | Thermodynamics, classical mechanics |
Introduction to Fields and Scalars
Fields describe physical quantities distributed across space and time, representing variable values at every point, while scalars are single-valued quantities with magnitude only, lacking direction. Common examples include temperature as a scalar field assigning a value to each location, and electric fields, which combine magnitude and direction but can also be represented through scalar potentials. Understanding the distinction between fields and scalars is fundamental in physics and mathematics for modeling spatially varying phenomena and analyzing uniform quantities.
Defining Scalars: Meaning and Examples
Scalars represent single-valued quantities in physics and mathematics, defined by magnitude alone without direction, such as temperature, mass, or time. Unlike fields, which assign a value or vector to every point in space, scalars provide a numeric value that remains constant regardless of position. Examples include electrical potential in electrostatics, density in fluid mechanics, and speed in kinematics.
Understanding Fields: Concepts and Types
Fields represent physical quantities defined at every point in space and time, with examples including electromagnetic, gravitational, and temperature fields, each described by mathematical functions that assign values to spatial coordinates. Scalar fields assign a single numeric value to each point, such as temperature or pressure, while vector fields associate a vector with magnitude and direction, like wind velocity or magnetic fields. Understanding the distinction between scalar and vector fields is crucial for modeling physical phenomena in physics, engineering, and applied mathematics.
Mathematical Representation of Scalars
Scalars are represented mathematically as single numerical values from a specified set, typically real or complex numbers, characterizing magnitude without direction. In contrast, fields assign such scalars to every point in a space, forming functions like scalar fields \( f: \mathbb{R}^n \to \mathbb{R} \). The mathematical representation of scalars as elements of a field underpins operations like addition and multiplication, facilitating the construction of vector spaces and advanced algebraic structures.
Mathematical Representation of Fields
A field is mathematically represented as a function assigning a scalar, vector, or tensor value to every point in space and time, often described using partial differential equations. Scalar fields map each spatial coordinate to a single scalar quantity, such as temperature or pressure, enabling straightforward representation as f(x, y, z, t). Complex physical phenomena like electromagnetic or gravitational effects require vector or tensor fields, represented by multi-component functions that capture magnitude and direction at each point.
Key Differences Between Fields and Scalars
Fields represent complex data structures with multiple components or dimensions, whereas scalars are single-value quantities with no internal structure. Fields can vary over space and time, often used to describe quantities like temperature or electromagnetic forces, while scalars are fixed numerical values such as mass or charge. The key difference lies in the multidimensional nature of fields compared to the simplicity of scalars.
Physical Examples: Scalar Quantities vs Field Quantities
Scalar quantities like temperature and mass describe physical properties with magnitude only, measured at a single point, whereas field quantities such as electric and magnetic fields assign a value to every point in space, varying continuously. Temperature represents a scalar field when mapped over a region, but as a standalone measurement, it is a scalar value. Electric field intensity exemplifies a vector field, emphasizing both magnitude and direction at each point, illustrating the complexity of field quantities beyond simple scalars.
Applications of Scalars in Science and Engineering
Scalars represent quantities with only magnitude, making them essential in various scientific and engineering applications such as temperature measurement, mass calculation, and electrical charge quantification. Unlike fields, which assign values throughout a region, scalars provide single-valued data critical for simplifying complex computations in thermodynamics, mechanics, and electrostatics. Their scalar nature allows straightforward integration into equations and models, facilitating analysis and design in heat transfer, fluid dynamics, and circuit theory.
Real-World Uses of Fields in Physics and Technology
Fields, such as electromagnetic and gravitational fields, describe how physical quantities vary in space and time, enabling the modeling of complex interactions in physics and engineering. Scalar quantities, represented by a single value like temperature or pressure, provide essential information but lack directionality, limiting their use in describing phenomena like force or velocity fields. Real-world applications of fields include wireless communication, where electromagnetic fields transmit signals, and medical imaging techniques like MRI, which rely on magnetic fields to produce detailed internal body images.
Conclusion: Importance of Fields and Scalars in Problem-Solving
Fields provide a comprehensive representation of spatially distributed data, enabling detailed analysis and solution of complex physical phenomena, while scalars offer simplicity and efficiency in quantifying singular magnitude values. Utilizing fields allows for modeling variations across regions, which is essential in simulations and engineering problems, whereas scalars facilitate straightforward calculations and comparisons. Understanding the complementary roles of fields and scalars empowers problem-solvers to choose the appropriate mathematical tools for accurate and efficient results.
Field Infographic
 libterm.com
libterm.com