Vector graphics use mathematical equations to create images that can be scaled infinitely without losing quality, making them ideal for logos and illustrations. Unlike raster images, vectors maintain crisp details regardless of size or resolution, ensuring your designs look professional on any medium. Explore the rest of the article to discover how vector technology can enhance your creative projects.
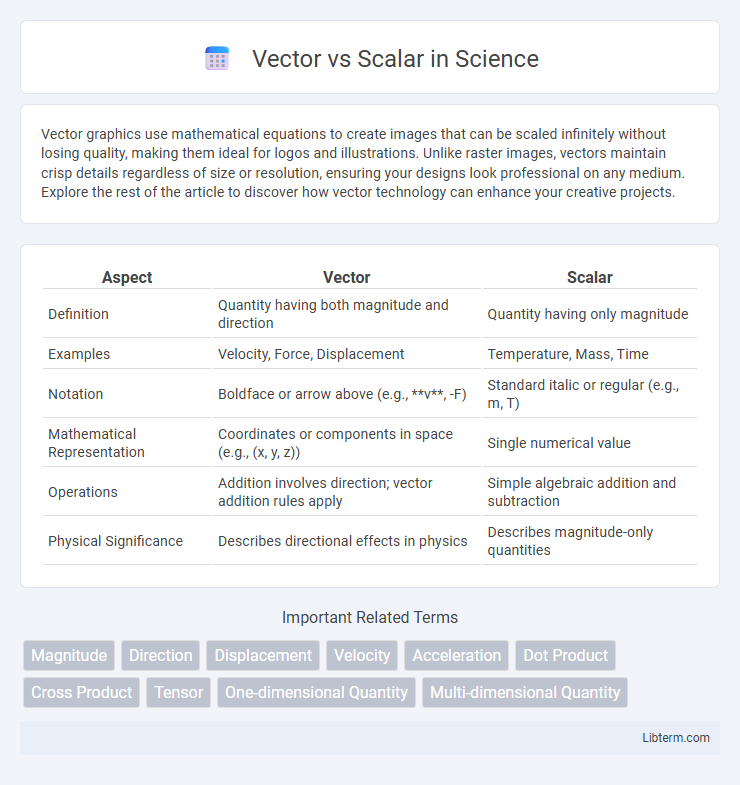
Table of Comparison
| Aspect | Vector | Scalar |
|---|---|---|
| Definition | Quantity having both magnitude and direction | Quantity having only magnitude |
| Examples | Velocity, Force, Displacement | Temperature, Mass, Time |
| Notation | Boldface or arrow above (e.g., v, -F) | Standard italic or regular (e.g., m, T) |
| Mathematical Representation | Coordinates or components in space (e.g., (x, y, z)) | Single numerical value |
| Operations | Addition involves direction; vector addition rules apply | Simple algebraic addition and subtraction |
| Physical Significance | Describes directional effects in physics | Describes magnitude-only quantities |
Introduction to Vectors and Scalars
Vectors represent quantities with both magnitude and direction, such as displacement, velocity, and force, while scalars have only magnitude, like temperature, mass, and time. Understanding vectors involves analyzing their components along coordinate axes, enabling precise description of physical phenomena in physics and engineering. Scalars are simpler to handle mathematically as they require only magnitude values without directional consideration.
Defining Scalars: Key Characteristics
Scalars are quantities defined by magnitude alone, such as temperature, mass, speed, and time, making them direction-independent. They are represented by real numbers and follow the rules of ordinary arithmetic without considering any directional properties. Scalar quantities are essential in physics and engineering for describing measurements that do not require vector components, simplifying calculations and analyses.
Understanding Vectors: Essential Properties
Vectors possess magnitude and direction, making them fundamental in representing physical quantities like velocity and force. Essential properties include direction, magnitude, and the ability to be added or subtracted using vector algebra. Scalar quantities differ by having only magnitude without direction, highlighting the critical role of vectors in multidimensional analysis.
Fundamental Differences Between Scalars and Vectors
Scalars are quantities defined solely by magnitude, such as temperature, mass, and time, while vectors possess both magnitude and direction, exemplified by velocity, force, and displacement. Scalars obey simple algebraic addition, whereas vectors require vector addition rules, including the triangle or parallelogram method. The fundamental difference lies in the directional component, making vectors essential for describing physical phenomena involving orientation, unlike scalars which represent magnitude-only properties.
Common Examples of Scalars in Everyday Life
Common examples of scalars in everyday life include temperature, time, mass, distance, and speed. These quantities have magnitude only and are described by a single numerical value without direction. Scalars are essential in daily activities such as measuring cooking ingredients, tracking elapsed time, weighing objects, and calculating travel distances.
Real-World Applications of Vectors
Vectors are essential in real-world applications such as physics, engineering, and computer graphics, where they represent quantities with both magnitude and direction, like velocity, force, and displacement. In navigation and robotics, vectors enable precise movement control and path planning by encoding directional data. Vector mathematics also underpins simulations and animations, enhancing the realism and accuracy of virtual environments.
Mathematical Operations: Scalar vs Vector
Scalars are quantities represented by a single numerical value and can be added, subtracted, multiplied, or divided using basic arithmetic operations. Vectors are quantities with both magnitude and direction, requiring vector-specific operations such as vector addition, subtraction, dot product, and cross product to combine or manipulate them. Scalar multiplication involves multiplying a vector by a scalar, scaling its magnitude without changing direction, while vector multiplication includes operations producing either scalar (dot product) or vector results (cross product), essential in physics and engineering calculations.
Visual Representation: Scalars and Vectors Explained
Scalars are quantities represented by a single numerical value and unit, such as temperature or mass, without any directional information. Vectors require both magnitude and direction for full representation, typically depicted as arrows in diagrams where the arrow length indicates magnitude and the arrowhead shows direction. Visualizing vectors helps in understanding physical phenomena involving forces, velocities, or displacement, while scalars remain visually simple and straightforward.
Importance of Scalars and Vectors in Physics
Scalars and vectors are fundamental in physics, with scalars representing quantities having only magnitude, such as mass, temperature, and energy, crucial for straightforward calculations and measurements. Vectors, possessing both magnitude and direction, like velocity, force, and acceleration, are essential for understanding physical phenomena involving direction-dependent processes. Mastery of scalars and vectors enables accurate modeling of real-world systems, facilitating advancements in mechanics, electromagnetism, and kinematics.
Choosing the Right Quantity: When to Use Vectors or Scalars
Choosing between vectors and scalars depends on the nature of the physical quantity being analyzed. Use vectors for quantities that involve both magnitude and direction, such as force, velocity, and displacement, to accurately represent spatial relationships and directional changes. Scalars are appropriate for quantities defined solely by magnitude, like temperature, mass, and speed, where direction does not impact the outcome.
Vector Infographic
 libterm.com
libterm.com