Quaternions are a number system that extends complex numbers, widely used in 3D computer graphics, robotics, and aerospace for representing rotations and orientations efficiently without suffering from gimbal lock. Their mathematical structure allows for smooth interpolation and real-time calculations crucial in animations and simulations. Explore the rest of the article to understand how quaternions can enhance Your projects and applications.
Table of Comparison
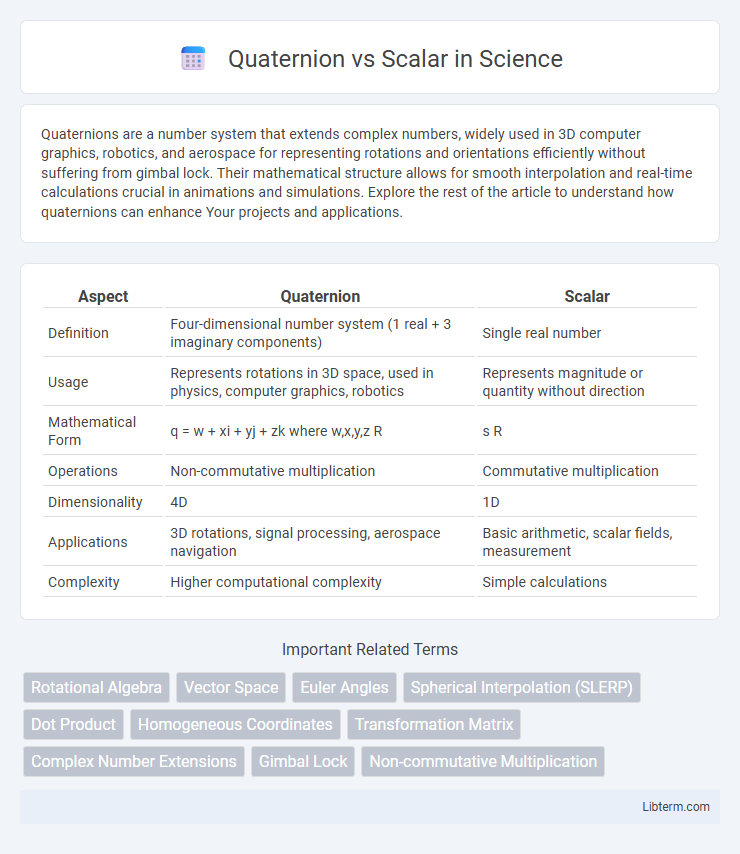
| Aspect | Quaternion | Scalar |
|---|---|---|
| Definition | Four-dimensional number system (1 real + 3 imaginary components) | Single real number |
| Usage | Represents rotations in 3D space, used in physics, computer graphics, robotics | Represents magnitude or quantity without direction |
| Mathematical Form | q = w + xi + yj + zk where w,x,y,z R | s R |
| Operations | Non-commutative multiplication | Commutative multiplication |
| Dimensionality | 4D | 1D |
| Applications | 3D rotations, signal processing, aerospace navigation | Basic arithmetic, scalar fields, measurement |
| Complexity | Higher computational complexity | Simple calculations |
Introduction to Quaternions and Scalars
Quaternions are hypercomplex numbers extending complex numbers, consisting of one real part and three imaginary units (i, j, k) used extensively in 3D rotations and computer graphics for their ability to represent orientations without gimbal lock. Scalars, in contrast, are single-valued quantities representing magnitude without direction, typically expressed as real numbers in mathematical and physical contexts. The fundamental distinction lies in quaternions' multidimensional structure enabling complex spatial transformations, whereas scalars provide basic magnitude information.
Fundamental Differences Between Quaternions and Scalars
Quaternions are four-dimensional hypercomplex numbers consisting of one real (scalar) part and three imaginary parts, represented as q = w + xi + yj + zk, enabling rotations in 3D space without gimbal lock. Scalars are single real numbers representing magnitude only, lacking directional or rotational components. Unlike scalars that support basic arithmetic operations, quaternions facilitate complex spatial transformations through quaternion multiplication and conjugation, defining orientation and rotation in computer graphics and robotics.
Mathematical Definitions and Properties
Quaternions are hypercomplex numbers consisting of one real part and three imaginary units, defined as q = a + bi + cj + dk, where i2 = j2 = k2 = ijk = -1, enabling representation of rotations in 3D space with non-commutative multiplication. Scalars are single real numbers representing magnitude only, following commutative algebraic properties and serving as the real-valued components within quaternion structure. The norm of a quaternion generalizes the scalar absolute value, calculated as (a2 + b2 + c2 + d2), facilitating quaternion normalization and inversion critical for 3D rotation transformations.
Applications in Computer Graphics and Robotics
Quaternions provide a compact and efficient representation of rotations in computer graphics and robotics, avoiding gimbal lock issues common with Euler angles. Their four-dimensional structure enables smooth interpolation through spherical linear interpolation (SLERP), crucial for realistic animation and precise robotic arm movement. Scalars lack the capability to represent rotations directly, limiting their applications in spatial transformations and orientation control.
Quaternion Algebra vs Scalar Arithmetic
Quaternion algebra extends scalar arithmetic by incorporating a four-dimensional number system consisting of one real part and three imaginary units, enabling the representation of complex rotations in 3D space. Unlike scalar arithmetic, which deals with single-dimensional values and ordinary multiplication and addition, quaternion algebra involves non-commutative multiplication rules for its components, allowing precise and efficient computations for spatial transformations. This distinct mathematical structure makes quaternions essential in fields such as computer graphics, robotics, and aerospace engineering, where robust and compact rotation calculations are critical.
Advantages of Using Quaternions
Quaternions offer significant advantages over scalars in representing rotations due to their ability to avoid gimbal lock and provide smooth interpolation through spherical linear interpolation (SLERP). Their four-dimensional structure enables compact and efficient computation of 3D orientations and transformations, making them essential in computer graphics, robotics, and aerospace applications. Quaternions also maintain numerical stability and conciseness compared to rotation matrices, enhancing performance in real-time systems.
Limitations and Challenges of Scalars
Scalars represent magnitude without direction, making them insufficient for describing complex spatial transformations such as rotations in three-dimensional space. Their inability to encode orientation or efficiently combine rotational data often leads to ambiguous or incomplete representations. This limitation challenges applications requiring precise and unambiguous rotational computations, where quaternions provide superior performance due to their four-dimensional structure and avoidance of gimbal lock.
Real-World Examples: Quaternion vs Scalar
Quaternions excel in 3D computer graphics, robotics, and aerospace for representing rotations and orientations without suffering from gimbal lock, unlike scalars that only express magnitude. Scalars are widely used in simple measurements such as temperature, mass, and distance, where direction or rotation is not involved. For example, a drone's flight control relies on quaternions for smooth rotational motion, while its battery level is tracked using a scalar value.
Choosing Between Quaternion and Scalar for Your Project
Choosing between quaternion and scalar depends on your project's need for representing rotations and orientations. Quaternions offer efficient, compact, and non-singular representation of 3D rotations, making them ideal for computer graphics, robotics, and aerospace applications. Scalars are simpler but lack the ability to encode complex orientation information, so they are better suited for basic numerical computations or where rotation representation is unnecessary.
Conclusion: Quaternion or Scalar?
Quaternions provide a robust mathematical framework for representing rotations in three-dimensional space, eliminating gimbal lock and enabling smooth interpolations, making them superior for applications in computer graphics, robotics, and aerospace. Scalars, while simpler and efficient for basic calculations, lack the ability to represent complex rotations and orientations effectively. Choosing quaternions over scalars is essential when precision and stability in 3D rotational computations are required.
Quaternion Infographic
 libterm.com
libterm.com