A derivative measures how a function changes as its input changes, representing the rate of change or slope at any given point. It plays a crucial role in fields such as physics, engineering, and economics by helping to analyze motion, optimize processes, and model dynamic systems. Explore the rest of this article to deepen your understanding of derivatives and their practical applications.
Table of Comparison
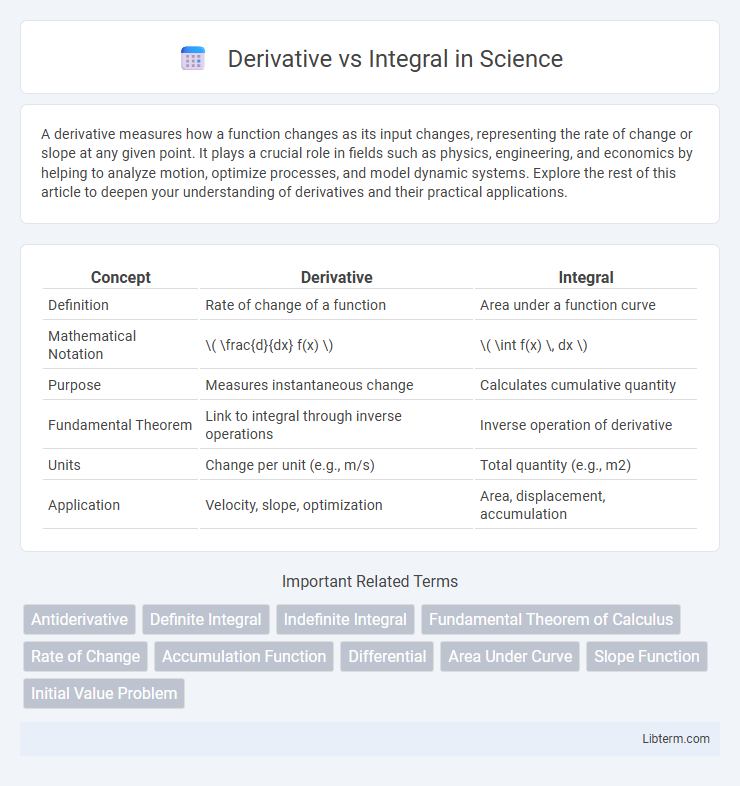
| Concept | Derivative | Integral |
|---|---|---|
| Definition | Rate of change of a function | Area under a function curve |
| Mathematical Notation | \( \frac{d}{dx} f(x) \) | \( \int f(x) \, dx \) |
| Purpose | Measures instantaneous change | Calculates cumulative quantity |
| Fundamental Theorem | Link to integral through inverse operations | Inverse operation of derivative |
| Units | Change per unit (e.g., m/s) | Total quantity (e.g., m2) |
| Application | Velocity, slope, optimization | Area, displacement, accumulation |
Understanding Derivatives: The Basics
Derivatives represent the rate of change of a function with respect to a variable, providing insight into the function's instantaneous slope. Calculating a derivative involves applying rules such as the power, product, and chain rules to functions, revealing critical points and behavior changes. Understanding derivatives is fundamental for analyzing motion, growth rates, and optimizing functions in calculus and applied mathematics.
Introduction to Integrals
Integrals represent the accumulation of quantities and are fundamental in calculus for finding areas under curves, total accumulated change, and solving differential equations. Unlike derivatives, which measure the instantaneous rate of change, integrals calculate the aggregate effect over an interval. The concept of integrals is divided into definite integrals, which provide numerical values for area, and indefinite integrals, representing families of antiderivatives.
Core Differences: Derivative vs Integral
Derivatives measure the instantaneous rate of change or slope of a function, capturing how a quantity varies at a specific point. Integrals represent the accumulation or total area under a curve, quantifying the aggregate value over an interval. While derivatives break down changes into infinitesimal increments, integrals sum these increments to reconstruct the original function or total quantity.
Mathematical Definitions and Notation
The derivative, denoted as f'(x) or dy/dx, represents the instantaneous rate of change of a function with respect to its variable, defined as the limit of the difference quotient. The integral, symbolized by f(x)dx, refers to the accumulation or area under the curve of a function, evaluated as the limit of Riemann sums. Both concepts are fundamental in calculus, with the derivative focusing on rates and slopes, and the integral on total accumulation and area calculations.
Visualizing Derivatives and Integrals
Visualizing derivatives involves interpreting the slope of the tangent line at any point on a function's graph, representing the instantaneous rate of change. Integrals are visualized as the area under a curve between two points, quantifying the total accumulation of a quantity. Graphical tools like slope fields and shaded region plots enhance the intuitive understanding of how derivatives and integrals relate to function behavior.
Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus bridges the concepts of derivatives and integrals by showing that differentiation and integration are inverse processes. It states that the integral of a function's derivative over an interval equals the function's net change on that interval, linking antiderivatives directly to definite integrals. This theorem provides a powerful tool for evaluating definite integrals using antiderivatives, streamlining many problems in calculus.
Applications of Derivatives in Real Life
Derivatives are essential in physics for calculating velocity and acceleration, enabling precise motion analysis. In economics, derivatives optimize profit by analyzing marginal cost and revenue changes. Engineering uses derivatives to model system dynamics and optimize performance in control systems and signal processing.
Practical Uses of Integrals
Integrals are essential in calculating areas under curves, determining accumulated quantities like distance traveled given velocity, and analyzing physical phenomena such as work done by a force or fluid flow. Unlike derivatives that measure instantaneous rates of change, integrals provide total accumulation over an interval, making them invaluable in engineering, economics, and physics for solving real-world problems involving continuous accumulation. Applications include computing volumes of solids of revolution, estimating consumer surplus in economics, and modeling population growth over time.
Common Misconceptions: Derivative vs Integral
Derivatives represent the rate of change of a function, while integrals calculate the accumulation of quantities over an interval. A common misconception is that derivatives and integrals are entirely separate concepts, whereas they are fundamentally linked by the Fundamental Theorem of Calculus, which shows integration as the inverse process of differentiation. Another misunderstanding is that derivatives only indicate increasing or decreasing behavior, but they also provide information on the rate and direction of change at any given point.
Choosing Between Derivative and Integral in Problem-Solving
Choosing between a derivative and an integral in problem-solving depends on the nature of the question: derivatives are used to find rates of change or slopes of functions, making them ideal for problems involving velocity, acceleration, or optimization. Integrals are suited for calculating accumulated quantities such as area under a curve, total distance traveled, or volume, especially when dealing with summation of continuous values. Understanding key concepts like differentiation rules, fundamental theorem of calculus, and boundary conditions helps determine the correct approach to solve real-world mathematical problems efficiently.
Derivative Infographic
 libterm.com
libterm.com