An antiderivative is a function whose derivative equals the original function, playing a key role in integral calculus and problem-solving involving areas and accumulation. Finding antiderivatives helps you reverse the differentiation process and solve differential equations effectively. Discover how mastering antiderivatives can enhance your understanding of calculus by reading the full article.
Table of Comparison
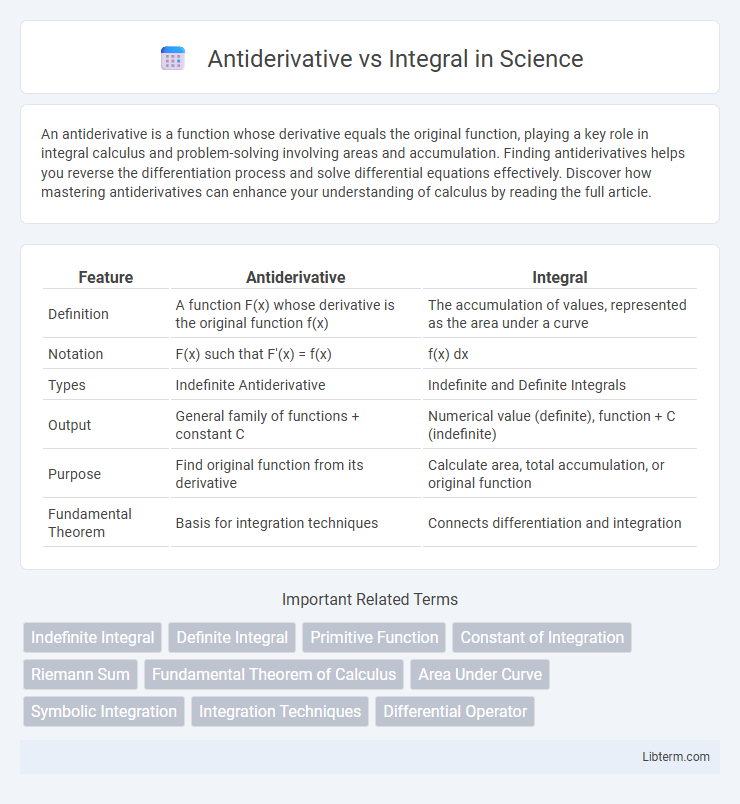
| Feature | Antiderivative | Integral |
|---|---|---|
| Definition | A function F(x) whose derivative is the original function f(x) | The accumulation of values, represented as the area under a curve |
| Notation | F(x) such that F'(x) = f(x) | f(x) dx |
| Types | Indefinite Antiderivative | Indefinite and Definite Integrals |
| Output | General family of functions + constant C | Numerical value (definite), function + C (indefinite) |
| Purpose | Find original function from its derivative | Calculate area, total accumulation, or original function |
| Fundamental Theorem | Basis for integration techniques | Connects differentiation and integration |
Understanding Antiderivatives: A Fundamental Overview
Antiderivatives represent the family of functions whose derivative equals a given function, serving as the foundational concept in calculus for reversing differentiation. The integral, specifically the definite integral, extends this by calculating the net area under a curve between two points, connecting antiderivatives with accumulation functions. Mastering antiderivatives is essential for understanding integral calculus, as every indefinite integral corresponds to an antiderivative plus a constant of integration.
What Is an Integral? Core Concepts Explained
An integral represents the accumulation of quantities and can be interpreted as the area under a curve on a graph of a function. It is a fundamental concept in calculus used to compute total values from rate functions, often denoted as the definite integral with limits or the indefinite integral without limits. Unlike an antiderivative, which is a function whose derivative equals the original function, an integral encompasses both antiderivatives and the process of calculating area or accumulated change over an interval.
Antiderivative vs Integral: Key Differences
Antiderivative represents a family of functions whose derivative equals the original function, while the integral encompasses both definite and indefinite forms, measuring area under a curve or representing accumulation. The antiderivative is an indefinite integral without limits, expressed with a constant of integration, whereas the definite integral evaluates the function between specific bounds yielding a numerical value. Key differences include the antiderivative as a general solution to differential problems, and the integral's broader application in calculating exact areas and accumulated quantities.
The Role of Indefinite Integrals in Calculus
Indefinite integrals represent the family of antiderivatives of a function, capturing all possible functions whose derivative matches the given function. In calculus, the indefinite integral serves as a fundamental tool for solving differential equations and determining accumulation functions without specified bounds. This concept bridges the gap between differentiation and integration, enabling the precise calculation of function families associated with rate changes.
Definite Integrals: Calculating Area and Accumulation
Definite integrals represent the exact accumulation of quantities, such as area under a curve, between specified limits, providing numerical values rather than general functions. Unlike antiderivatives, which yield families of functions representing indefinite integrals, definite integrals compute precise totals essential in physics, engineering, and probability. Properties like additivity and linearity enable efficient evaluation of definite integrals through methods such as the Fundamental Theorem of Calculus.
Connection Between Antiderivatives and Integrals
Antiderivatives and integrals are fundamentally connected through the Fundamental Theorem of Calculus, which states that the definite integral of a function over an interval is equal to the difference of its antiderivative evaluated at the endpoints. An antiderivative of a function is any function whose derivative matches the original function, forming the basis for calculating indefinite integrals. Definite integrals represent the net area under the curve defined by the function, while antiderivatives provide a family of functions that can be used to evaluate those integrals efficiently.
Examples: Solving Antiderivatives and Integrals
Solving antiderivatives often involves finding a function F(x) such that F'(x) equals the original function f(x), for example, the antiderivative of f(x) = 2x is F(x) = x2 + C, where C represents the constant of integration. For integrals, definite integrals like 01 2x dx calculate the area under the curve by evaluating F(1) - F(0) = 12 - 02 = 1, illustrating the application of the Fundamental Theorem of Calculus. Indefinite integrals represent general antiderivatives, whereas definite integrals provide numerical values corresponding to the accumulated quantity over an interval.
Common Misconceptions: Antiderivative vs Integral
Many confuse antiderivatives with definite integrals, but an antiderivative represents a family of functions whose derivative is the original function, whereas an integral quantifies the area under a curve between specified limits. Another misconception is that antiderivatives always include a constant of integration, while definite integrals produce numerical values without any additional constants. Understanding that the antiderivative is an indefinite integral highlighting function families, and the integral evaluates accumulation over intervals clarifies their distinct mathematical roles.
Applications in Science and Engineering
Antiderivatives provide fundamental solutions to differential equations, essential for modeling physical phenomena such as motion and heat transfer in engineering. Integrals, especially definite integrals, quantify cumulative quantities like area, volume, and work done, playing a crucial role in fields like electromagnetism and fluid dynamics. Both concepts enable precise calculations in system analysis, control theory, and signal processing, driving advancements in technology and scientific research.
Summary: Choosing the Right Approach
Antiderivatives represent the family of functions whose derivative equals the given function, while integrals compute the accumulated area under a curve, often expressed as definite or indefinite integrals. Choosing the right approach depends on whether you need a general formula (antiderivative) or a specific numerical value over an interval (definite integral). Understanding the distinction between these concepts is crucial for accurate application in calculus problems and real-world scenarios.
Antiderivative Infographic
 libterm.com
libterm.com