Diameter measures the straight line passing through the center of a circle, connecting two points on its boundary. Understanding diameter is essential in geometry, engineering, and everyday measurements to determine size and capacity. Explore the rest of the article to discover how diameter influences various applications and calculations.
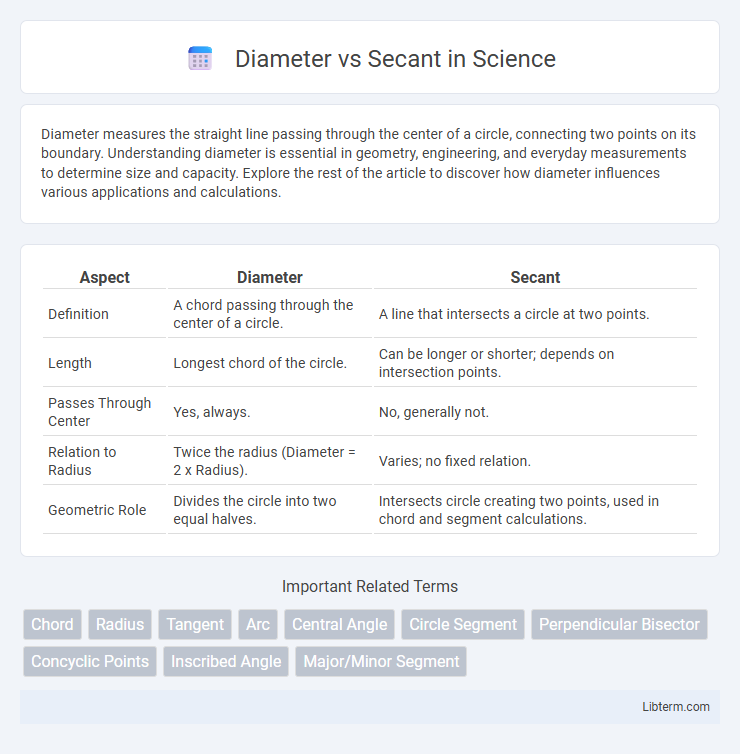
Table of Comparison
| Aspect | Diameter | Secant |
|---|---|---|
| Definition | A chord passing through the center of a circle. | A line that intersects a circle at two points. |
| Length | Longest chord of the circle. | Can be longer or shorter; depends on intersection points. |
| Passes Through Center | Yes, always. | No, generally not. |
| Relation to Radius | Twice the radius (Diameter = 2 x Radius). | Varies; no fixed relation. |
| Geometric Role | Divides the circle into two equal halves. | Intersects circle creating two points, used in chord and segment calculations. |
Understanding the Basics: Diameter and Secant Defined
The diameter of a circle is a straight line segment passing through the center, connecting two points on the circle's circumference, and representing the longest possible chord. A secant is a line that intersects the circle at two distinct points but does not necessarily pass through the center. Understanding these definitions clarifies that while all diameters are secants, not all secants are diameters, highlighting their fundamental geometric differences.
Key Differences Between Diameter and Secant
A diameter is a chord that passes through the center of a circle, making it the longest possible chord and dividing the circle into two equal halves. A secant is a line that intersects a circle at two distinct points but does not necessarily pass through the center. Key differences include that every diameter is a secant, but not every secant is a diameter, and diameters have a fixed length equal to twice the radius, while secants can vary in length depending on the intersection points.
Mathematical Properties of Diameters
The diameter of a circle is a line segment passing through the center and connecting two points on the circumference, having twice the length of the radius. It uniquely divides the circle into two equal semicircles and serves as the longest possible chord in the circle. Unlike secants that intersect the circle at two points but do not necessarily pass through the center, the diameter's central positioning directly influences circle symmetry and simplifies calculations involving circumference and area.
Mathematical Properties of Secants
A secant is a line that intersects a circle at exactly two points, extending beyond the circle's boundary, while a diameter is a special type of chord passing through the circle's center, dividing it into two equal halves. Secants have important mathematical properties, such as the Secant-Secant Power Theorem, which states that the product of the lengths of the whole secant segment and its external segment is constant for two secants drawn from the same external point. Unlike diameters, secants do not necessarily pass through the circle's center, and their length varies depending on the points of intersection with the circle.
Geometric Representation: Diameter vs Secant
A diameter of a circle is a straight line segment passing through the center, connecting two points on the circle's circumference, representing the longest possible chord. In contrast, a secant intersects the circle at two points but does not necessarily pass through the center, extending infinitely in both directions outside the circle. The geometric representation distinguishes the diameter as a specific type of chord, whereas the secant functions as a line cutting through the circle, with the diameter always measuring twice the radius.
Role of Diameter and Secant in Circle Equations
The diameter of a circle, defined as the longest chord passing through the center, plays a crucial role in circle equations by determining the circle's radius, which is half the diameter length. Secants, as lines intersecting the circle at two points, are essential in geometric problems involving chord lengths and segment calculations within circle equations. Understanding the relationship between diameter and secants enables precise derivation of formulas related to circle geometry, including chord lengths and sector areas.
Applications of Diameter in Geometry and Real Life
Diameter plays a crucial role in geometry by defining the longest chord of a circle and aiding in the calculation of radius and circumference, essential for solving problems involving circles and spheres. In real life, diameters are critical in engineering and manufacturing, ensuring the precise sizing of pipes, wheels, and lenses for optimal performance. The consistent use of diameter measurements facilitates quality control and design accuracy in various industries such as automotive, construction, and optics.
Applications of Secant in Geometry and Real Life
The secant line plays a crucial role in geometry by intersecting a circle at two points, enabling the calculation of segment lengths and angles that aid in solving complex geometric problems. In real life, the concept of secant is applied in engineering fields such as signal processing and optics, where secant functions help model wave behaviors and light refraction. Secants also facilitate the measurement of distances and angles in surveying and navigation by approximating curved paths with linear segments.
Diameter vs Secant: Common Misconceptions
Diameter is often confused with a secant; however, a diameter is a special type of chord that passes through the center of a circle, while a secant intersects the circle at two distinct points without necessarily passing through the center. A common misconception is that all secants are diameters, but only those chords dividing the circle into two equal halves qualify as diameters. Understanding that the diameter is the longest chord and a secant can extend beyond the circle helps clarify their distinct geometric roles.
Summary: Choosing Diameter or Secant for Problem Solving
Choosing between diameter and secant depends on the geometric context and problem requirements. A diameter, being the longest chord passing through the circle's center, is ideal for problems involving maximum distance or symmetry within the circle. Secants, intersecting the circle at two points without passing through the center, are useful for solving problems related to angle measures, segment lengths, and external intersections.
Diameter Infographic
 libterm.com
libterm.com