Regular exercise improves cardiovascular health, boosts energy levels, and enhances mental clarity. Establishing a consistent workout routine can help you maintain a healthy weight and reduce the risk of chronic diseases. Discover effective strategies to make fitness a sustainable part of your lifestyle by reading the rest of the article.
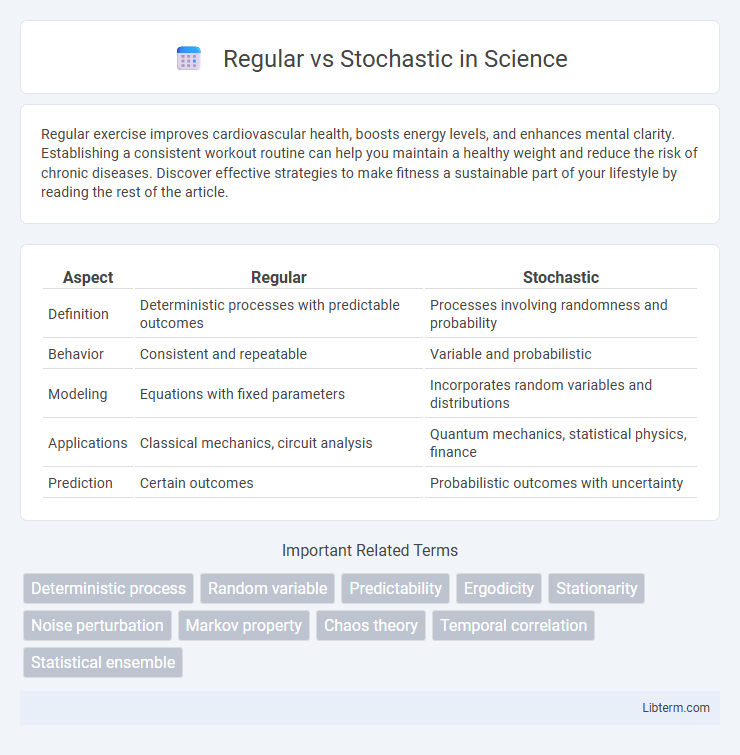
Table of Comparison
| Aspect | Regular | Stochastic |
|---|---|---|
| Definition | Deterministic processes with predictable outcomes | Processes involving randomness and probability |
| Behavior | Consistent and repeatable | Variable and probabilistic |
| Modeling | Equations with fixed parameters | Incorporates random variables and distributions |
| Applications | Classical mechanics, circuit analysis | Quantum mechanics, statistical physics, finance |
| Prediction | Certain outcomes | Probabilistic outcomes with uncertainty |
Introduction to Regular vs Stochastic
Regular processes follow deterministic rules with predictable outcomes, while stochastic processes incorporate randomness and uncertainty in their behavior. In probability theory and statistics, stochastic models represent systems influenced by random variables, contrasting with regular models that assume fixed patterns. Understanding these differences is crucial in fields like finance, physics, and machine learning, where accurate modeling of uncertainty impacts decision-making and predictions.
Defining Regular and Stochastic Processes
Regular processes are deterministic systems where outcomes can be precisely predicted based on initial conditions, often described by fixed mathematical rules or algorithms. Stochastic processes involve randomness and uncertainty, characterized by probabilistic behaviors that evolve over time, such as Markov chains or Poisson processes. Defining these processes hinges on the predictability of their state transitions: regular processes follow known patterns, while stochastic processes depend on probability distributions for future states.
Key Differences: Regular vs Stochastic
Regular processes follow deterministic rules, producing predictable and consistent outcomes, while stochastic processes incorporate randomness and uncertainty, resulting in variable and probabilistic results. The key difference lies in predictability: regular models yield fixed outputs from given inputs, whereas stochastic models generate different outcomes due to inherent randomness. Applications of regular models are common in well-defined environments, whereas stochastic models are essential in fields like finance and weather forecasting where uncertainty plays a critical role.
Applications of Regular Systems
Regular systems, characterized by deterministic behavior and predictable output, are widely applied in industrial automation where consistent performance is crucial. These systems excel in manufacturing processes, robotic control, and signal processing, ensuring accuracy and efficiency. Their reliability makes them essential for applications requiring precise timing and repeatability.
Applications of Stochastic Systems
Stochastic systems play a critical role in modeling complex phenomena in finance, such as option pricing and risk assessment, by incorporating randomness and uncertainty into predictive algorithms. They are essential in engineering for designing adaptive control systems that respond to unpredictable environmental changes, enhancing robustness and reliability. In biological sciences, stochastic models facilitate the understanding of gene expression variability and population dynamics, capturing inherent randomness in natural processes for more accurate simulations.
Mathematical Foundations of Regularity
Regular frameworks rely on deterministic patterns governed by precise mathematical functions such as continuity, differentiability, and linearity to ensure predictable system behavior. Stochastic models incorporate probabilistic elements characterized by random variables, probability distributions, and statistical dependence, emphasizing uncertainty and variability in outcomes. Mathematical foundations of regularity emphasize stability through eigenvalues, norms, and fixed points, contrasting with stochastic analysis which depends on expectation, variance, and Markov processes.
Probability and Uncertainty in Stochastic Models
Stochastic models incorporate probability distributions to capture uncertainty and random variations in system behavior, making them essential for accurately modeling real-world processes with inherent randomness. Unlike regular deterministic models that produce fixed outputs, stochastic models provide probabilistic outcomes, allowing for risk assessment and variability analysis. The use of probability theory in stochastic models enhances decision-making by quantifying uncertainty and enabling simulations of multiple possible scenarios.
Real-World Examples: Regular vs Stochastic
Regular processes follow fixed, predictable patterns exemplified by HVAC systems operating on set schedules for consistent climate control. Stochastic processes incorporate randomness, seen in stock market fluctuations where prices vary unpredictably due to economic events and investor behavior. Weather forecasting combines both, using regular atmospheric cycles alongside stochastic modeling of unpredictable factors like storms and temperature variations.
Advantages and Limitations of Each Approach
Regular algorithms offer deterministic results with predictable performance and are easier to debug, making them suitable for well-defined problems. Stochastic methods introduce randomness, providing robustness against local optima and flexibility in exploring complex solution spaces but can lead to variable outcomes and longer convergence times. Each approach balances precision and adaptability differently, influencing their effectiveness depending on the problem context.
Choosing Between Regular and Stochastic Methods
Choosing between regular and stochastic methods depends on dataset size and computational resources. Regular methods, such as batch gradient descent, process the entire dataset per iteration, making them suitable for smaller datasets where precision is critical. Stochastic methods, including stochastic gradient descent (SGD), update parameters using individual or mini-batches of samples, offering faster convergence and scalability for large datasets or real-time applications.
Regular Infographic
 libterm.com
libterm.com