A tangent is a straight line that touches a curve at exactly one point without crossing it. This concept is fundamental in geometry and calculus, where it helps analyze the slope and behavior of curves at specific points. Explore the rest of the article to deepen your understanding of tangents and their applications.
Table of Comparison
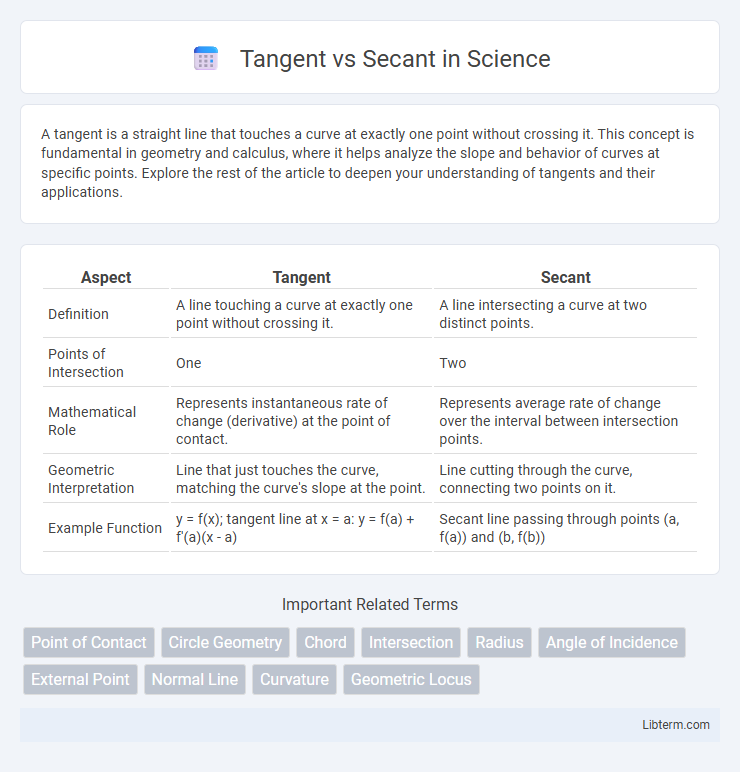
| Aspect | Tangent | Secant |
|---|---|---|
| Definition | A line touching a curve at exactly one point without crossing it. | A line intersecting a curve at two distinct points. |
| Points of Intersection | One | Two |
| Mathematical Role | Represents instantaneous rate of change (derivative) at the point of contact. | Represents average rate of change over the interval between intersection points. |
| Geometric Interpretation | Line that just touches the curve, matching the curve's slope at the point. | Line cutting through the curve, connecting two points on it. |
| Example Function | y = f(x); tangent line at x = a: y = f(a) + f'(a)(x - a) | Secant line passing through points (a, f(a)) and (b, f(b)) |
Understanding Tangents: A Basic Overview
Tangents are straight lines that touch a curve or circle at exactly one point without crossing it, representing the instantaneous direction of the curve at that point. The tangent line's slope at the point of contact corresponds to the derivative of the curve's equation, providing critical insights in calculus for understanding rates of change. In contrast, a secant line intersects the curve at two or more points, offering an average rate of change between those points rather than an instantaneous measure.
Exploring Secants: Key Definitions
Secants are lines that intersect a curve at two distinct points, playing a crucial role in understanding average rates of change in calculus. The secant line between points \( A(x_1, y_1) \) and \( B(x_2, y_2) \) on a function \( f(x) \) calculates the average slope as \( \frac{f(x_2) - f(x_1)}{x_2 - x_1} \). Secants provide foundational insights for approximating tangents and analyzing instantaneous rates of change in mathematical analysis.
Geometric Differences: Tangent vs Secant
A tangent line touches a curve at exactly one point, creating a perpendicular relationship with the radius at the point of contact in circles, which highlights its unique geometric property of having only one intersection. In contrast, a secant line intersects the curve at two distinct points, effectively cutting through the shape and providing a segment that connects these points along the curve. This fundamental difference in how each line interacts with the curve defines their respective roles in geometry, particularly in circle theorems and analytic geometry applications.
Mathematical Equations of Tangents
The tangent line to a curve at a point is defined by the equation \( y = f(a) + f'(a)(x - a) \), where \( f'(a) \) represents the derivative of the function \( f \) at \( x = a \), indicating the slope of the tangent. In contrast, the secant line through points \( (a, f(a)) \) and \( (b, f(b)) \) is given by \( y = f(a) + \frac{f(b) - f(a)}{b - a}(x - a) \), representing the average rate of change between those points. The tangent's equation captures instantaneous change, making it fundamental in differential calculus for analyzing function behavior locally.
Mathematical Formulation of Secants
The mathematical formulation of a secant line is defined by the equation \( y = f(a) + \frac{f(b) - f(a)}{b - a} (x - a) \), representing the average rate of change of the function \( f(x) \) between points \( a \) and \( b \). Unlike a tangent line, which touches the curve at a single point and represents the instantaneous rate of change, the secant line intersects the curve at two distinct points. This formulation is fundamental in calculus, particularly in the definition of the derivative and in analyzing the behavior of functions over intervals.
Real-World Applications: Tangents and Secants
Tangents are critical in engineering for defining the exact point where a curve and a line meet, essential in designing roads and railway tracks for smooth transitions. Secant lines play a key role in navigation and astronomy by approximating the slopes of curves to calculate distances and angles between celestial bodies. Both concepts underpin the development of algorithms in computer graphics, enabling precise rendering of shapes and motion simulations.
Comparing Properties: Tangent vs Secant
A tangent line touches a circle at exactly one point, maintaining a perpendicular relationship with the radius at that point, while a secant line intersects the circle at two distinct points, creating a chord between those intersections. The length of the tangent segment from an external point equals the square root of the product of the secant segment's external part and its entire length, known as the Power of a Point Theorem. In calculus, the tangent line represents the instantaneous rate of change or slope at a single point on a curve, whereas a secant line provides the average rate of change between two points.
Intersection Points: Tangent and Secant Lines
Tangent lines intersect a circle at exactly one point called the point of tangency, where the line just touches the curve without crossing it. Secant lines pass through the circle, intersecting it at two distinct points, creating a chord between them. The distinction in their intersection points is fundamental in geometry, influencing properties such as angles, arcs, and segment lengths related to the circle.
Visualizing Tangents and Secants in Circles
Tangent lines touch a circle at exactly one point, creating a right angle with the radius at the point of contact, clearly illustrating the concept of tangency. Secant lines intersect a circle at two distinct points, cutting through the circle and demonstrating the chord created by their intersections. Visualizing these lines highlights the fundamental geometric relationships and differences between tangents, which graze the circle, and secants, which slice through it.
Summary: Which One to Use and When
Tangent lines are best suited for finding the instantaneous rate of change or slope of a curve at a single point, making them essential in calculus and physics for velocity and optimization problems. Secant lines are ideal for approximating average rates of change between two points on a curve, frequently used in numerical methods and when calculating average velocity or slope over an interval. Choose tangent for precise local analysis and secant for broader interval approximations.
Tangent Infographic
 libterm.com
libterm.com