Graphs visually represent data relationships, making complex information easier to understand and analyze. They help identify trends, patterns, and outliers quickly, enhancing decision-making processes in various fields. Explore the rest of the article to see how different types of graphs can optimize your data interpretation.
Table of Comparison
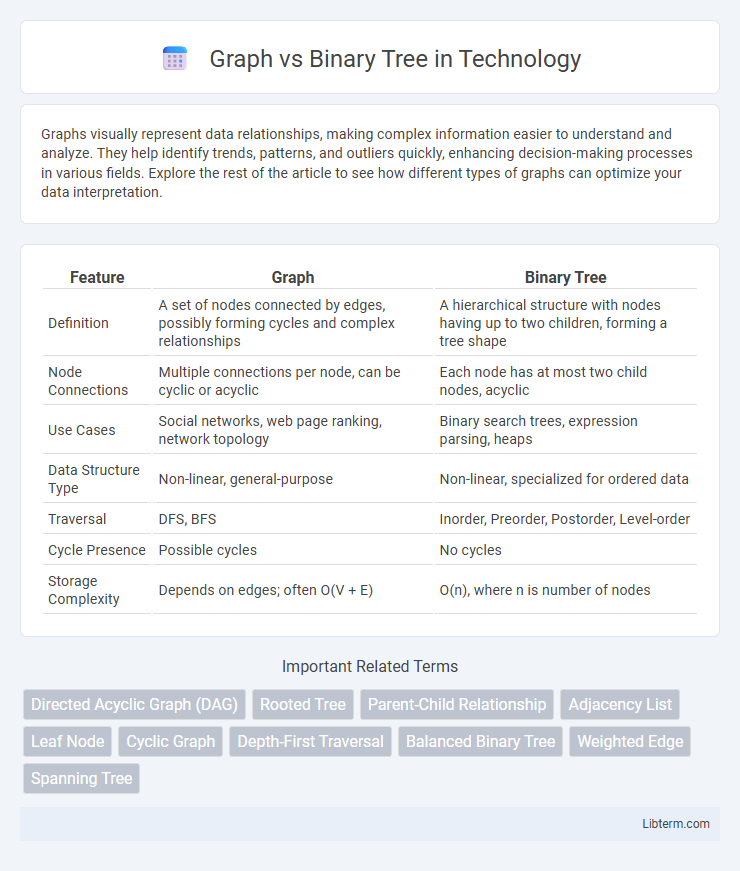
| Feature | Graph | Binary Tree |
|---|---|---|
| Definition | A set of nodes connected by edges, possibly forming cycles and complex relationships | A hierarchical structure with nodes having up to two children, forming a tree shape |
| Node Connections | Multiple connections per node, can be cyclic or acyclic | Each node has at most two child nodes, acyclic |
| Use Cases | Social networks, web page ranking, network topology | Binary search trees, expression parsing, heaps |
| Data Structure Type | Non-linear, general-purpose | Non-linear, specialized for ordered data |
| Traversal | DFS, BFS | Inorder, Preorder, Postorder, Level-order |
| Cycle Presence | Possible cycles | No cycles |
| Storage Complexity | Depends on edges; often O(V + E) | O(n), where n is number of nodes |
Introduction to Graphs and Binary Trees
Graphs and binary trees are fundamental data structures in computer science, each serving distinct purposes; a graph consists of nodes connected by edges, representing complex relationships, while a binary tree is a hierarchical structure where each node has at most two children. Graphs can model networks such as social media or transportation systems, allowing cycles and multiple connections, whereas binary trees are optimized for efficient searching and sorting operations. Understanding their differences is crucial for choosing the appropriate data structure based on the problem's requirements and performance considerations.
Fundamental Definitions
A graph is a collection of nodes, called vertices, connected by edges that can be either directed or undirected, allowing complex relationships and cycles. A binary tree is a hierarchical data structure where each node has at most two children, termed left and right, ensuring a strict parent-child relationship without cycles. Graphs enable representation of more general connections, while binary trees are specialized for ordered, acyclic hierarchical data.
Key Structural Differences
Graphs consist of a set of vertices connected by edges and can be directed or undirected, allowing cycles and multiple connections between nodes. Binary trees are a specialized type of tree data structure where each node has at most two children, known as the left and right child, and must not contain cycles, ensuring a hierarchical organization. The key structural difference lies in graphs' flexibility in connectivity and possible cycles, while binary trees enforce a strict parent-child relationship without cycles or multiple paths.
Node Connectivity Comparison
Graph nodes can connect to multiple nodes with no strict hierarchical structure, allowing cycles and complex connectivity patterns. Binary tree nodes have a maximum of two children, enforcing a strict hierarchical structure with no cycles and a single parent for each node except the root. This fundamental difference results in graphs supporting versatile connectivity and relationships, while binary trees maintain ordered, acyclic parent-child links optimized for efficient search and traversal.
Traversal Techniques
Graph traversal techniques include Depth-First Search (DFS) and Breadth-First Search (BFS), both capable of visiting nodes in any order due to the non-linear, interconnected nature of graphs. Binary tree traversal primarily involves In-order, Pre-order, and Post-order methods, which systematically visit nodes based on the left-child, root, and right-child relationships inherent in tree structures. Graphs require tracking visited nodes to handle cycles, while binary trees do not face this complexity due to their hierarchical acyclic nature.
Use Cases and Applications
Graphs excel in modeling complex networks such as social media interactions, transportation systems, and communication networks due to their ability to represent relationships with cycles and multiple connections between nodes. Binary trees are ideal for hierarchical data structures like binary search trees used in database indexing, expression parsing, and efficient sorting algorithms. While graphs handle diverse connectivity for route optimization and recommendation systems, binary trees provide structured organization for quick data retrieval and decision-making processes.
Advantages and Limitations
Graphs offer the advantage of representing complex relationships with multiple connections between nodes, supporting both directed and undirected edges, making them ideal for modeling networks like social connections and communication systems. Binary trees excel in hierarchical data organization with efficient search, insertion, and deletion operations due to their structured parent-child relationship, commonly used in sorting algorithms and binary search trees. However, graphs can be computationally intensive and more complex to traverse or analyze due to cycles and multiple paths, while binary trees have limitations in representing non-hierarchical, many-to-many relationships and can become unbalanced, affecting performance.
Storage and Memory Considerations
Graphs typically require more memory than binary trees due to the need to store adjacency information for each node, which can involve adjacency lists or matrices depending on graph density and structure. Binary trees have a more predictable and compact memory layout, often using pointers for left and right child nodes, leading to efficient storage particularly for hierarchical data. The choice between graph and binary tree structures impacts storage overhead and memory access patterns, influencing performance based on the specific application and data relationships.
Performance and Complexity
Graphs offer flexible connections between nodes with potentially multiple edges, resulting in higher computational complexity for traversal algorithms, typically O(V + E) where V is vertices and E is edges. Binary trees, structured with at most two child nodes, provide efficient search operations such as binary search trees with average time complexity of O(log n). Performance in binary trees is generally optimized for hierarchical data with predictable branching, while graphs handle complex relationships but require more resources for pathfinding and cycle detection.
Choosing Between Graphs and Binary Trees
Choosing between graphs and binary trees depends on the complexity and nature of data relationships; graphs efficiently represent complex networks with non-hierarchical connections, while binary trees excel in hierarchically structured data such as search trees and expression parsing. Graphs handle cycles, multiple paths, and diverse connectivity, making them suitable for social networks, routing algorithms, and dependency analysis. Binary trees provide faster search, insert, and delete operations in sorted data sets, benefiting applications like binary search trees, heaps, and syntax trees.
Graph Infographic
 libterm.com
libterm.com