Agent-based modeling simulates the interactions of autonomous agents to analyze complex systems and emergent phenomena in fields like economics, biology, and social sciences. This approach helps uncover patterns and behaviors that traditional models might miss, offering deeper insights into dynamic environments. Explore the rest of the article to understand how agent-based modeling can enhance your analysis and decision-making processes.
Table of Comparison
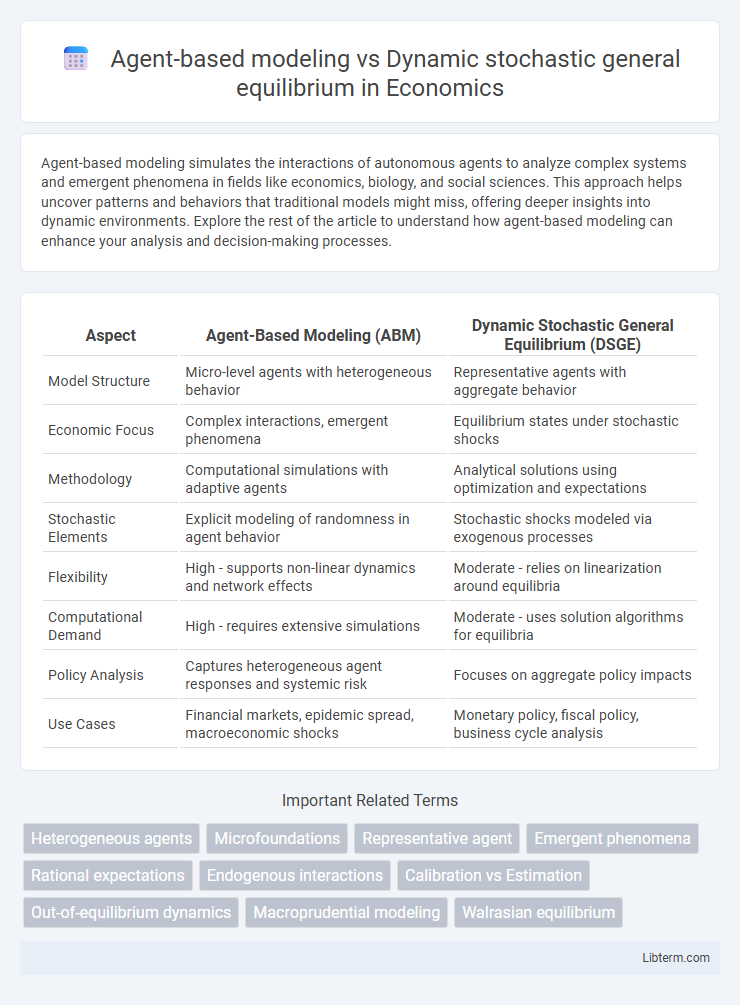
| Aspect | Agent-Based Modeling (ABM) | Dynamic Stochastic General Equilibrium (DSGE) |
|---|---|---|
| Model Structure | Micro-level agents with heterogeneous behavior | Representative agents with aggregate behavior |
| Economic Focus | Complex interactions, emergent phenomena | Equilibrium states under stochastic shocks |
| Methodology | Computational simulations with adaptive agents | Analytical solutions using optimization and expectations |
| Stochastic Elements | Explicit modeling of randomness in agent behavior | Stochastic shocks modeled via exogenous processes |
| Flexibility | High - supports non-linear dynamics and network effects | Moderate - relies on linearization around equilibria |
| Computational Demand | High - requires extensive simulations | Moderate - uses solution algorithms for equilibria |
| Policy Analysis | Captures heterogeneous agent responses and systemic risk | Focuses on aggregate policy impacts |
| Use Cases | Financial markets, epidemic spread, macroeconomic shocks | Monetary policy, fiscal policy, business cycle analysis |
Introduction to Agent-Based Modeling and DSGE
Agent-based modeling (ABM) simulates interactions of autonomous agents to assess complex economic phenomena, emphasizing heterogeneity and emergent behavior in markets. Dynamic stochastic general equilibrium (DSGE) models rely on representative agents optimizing decisions under uncertainty, rooted in microeconomic theory and general equilibrium concepts. ABM offers flexibility in capturing non-linear interactions and adaptation, whereas DSGE provides a structured framework for policy analysis through equilibrium conditions and stochastic shocks.
Core Principles of Agent-Based Models
Agent-based models (ABMs) emphasize heterogeneous agents who interact locally and adapt their behaviors based on rules and feedback, capturing emergent phenomena from micro-level interactions. ABMs rely on decentralized decision-making, bounded rationality, and explicit representation of agent heterogeneity, contrasting with the representative agent assumption in Dynamic Stochastic General Equilibrium (DSGE) models. This core principle allows ABMs to simulate complex dynamics, non-linearities, and out-of-equilibrium behaviors that DSGE often cannot address.
Core Principles of Dynamic Stochastic General Equilibrium
Dynamic Stochastic General Equilibrium (DSGE) models are grounded in microeconomic foundations, assuming rational agents optimizing intertemporally under uncertainty, with markets clearing at all times. Core principles emphasize equilibrium conditions derived from agents' optimizing behavior, incorporating stochastic shocks to capture economic fluctuations. This framework contrasts with agent-based modeling by focusing on aggregate equilibrium outcomes rather than heterogeneous individual interactions.
Modeling Economic Agents: Heterogeneity vs. Representative Agents
Agent-based modeling captures economic agents' heterogeneity by simulating individual behaviors and interactions, enabling rich analysis of decentralized decision-making and emergent macroeconomic patterns. Dynamic stochastic general equilibrium (DSGE) models use representative agents to simplify economic dynamics, emphasizing aggregate relationships and equilibrium conditions under stochastic shocks. The contrast between agent-based models' micro-level diversity and DSGE's aggregate representation highlights differing approaches to understanding economic complexity and policy impacts.
Capturing Nonlinearities and Emergent Phenomena
Agent-based modeling excels at capturing nonlinearities and emergent phenomena by simulating interactions among heterogeneous agents, allowing complex system behavior to arise spontaneously. Dynamic Stochastic General Equilibrium (DSGE) models rely on representative agents and rational expectations, often linearizing equations, which limits their ability to fully represent nonlinear dynamics and emergent outcomes. The flexibility of agent-based models makes them particularly suited for exploring systemic risks, market crashes, and adaptive behaviors that conventional DSGE frameworks may overlook.
Calibration, Validation, and Real-World Data
Agent-based modeling calibrates parameters through empirical micro-level data, enabling realistic simulation of heterogeneous agent behaviors, while Dynamic Stochastic General Equilibrium (DSGE) models often rely on macroeconomic aggregates and structural assumptions for calibration. Validation in agent-based models emphasizes replicating observed microeconomic patterns and emergent phenomena, whereas DSGE models undergo rigorous testing against aggregate time-series data and policy shock responses. Real-world data integration is more flexible in agent-based approaches, allowing incorporation of detailed agent interactions, whereas DSGE models prioritize consistency with equilibrium conditions and macroeconomic theory.
Policy Analysis Capabilities: ABM vs DSGE
Agent-based modeling (ABM) allows for capturing heterogeneous agent behaviors and interactions in a decentralized manner, enabling detailed analysis of policy impacts on micro-level dynamics and emergent macro outcomes. Dynamic stochastic general equilibrium (DSGE) models rely on representative agents optimizing intertemporal utility under rational expectations, offering analytical tractability for evaluating aggregate policy effects within equilibrium frameworks. ABM provides greater flexibility in simulating non-linearities, network effects, and behavioral adaptation, while DSGE models excel in structural interpretation and counterfactual policy experiments grounded in general equilibrium constraints.
Computational Requirements and Scalability
Agent-based modeling (ABM) demands significant computational power due to the need to simulate interactions of numerous heterogeneous agents with complex behaviors, often resulting in high memory usage and longer processing times. Dynamic stochastic general equilibrium (DSGE) models typically require less computational resources since they rely on solving systems of equations representing aggregate economic relationships, which scales more efficiently with model complexity. Scalability in ABM is limited by the exponential growth of agent interactions and state variables, whereas DSGE models benefit from mathematical optimization techniques that allow easier handling of larger-scale economic simulations.
Criticisms and Limitations of Each Approach
Agent-based modeling faces criticism for its high computational complexity and challenges in calibrating parameters, which can limit its predictive accuracy and generalizability. Dynamic stochastic general equilibrium models often receive criticism for their reliance on strong assumptions, such as market clearing and representative agents, which may oversimplify real economic behaviors and ignore heterogeneity. Both approaches struggle with balancing model tractability and realism, impacting their effectiveness in capturing dynamic economic phenomena under uncertainty.
Future Directions in Macroeconomic Modeling
Future directions in macroeconomic modeling emphasize integrating agent-based modeling (ABM) to capture micro-level heterogeneity and nonlinear interactions often abstracted in dynamic stochastic general equilibrium (DSGE) frameworks. Advances in computational power and data availability enable hybrid models combining DSGE's rigorous theoretical foundations with ABM's realistic agent behavior and adaptive learning processes. This integration aims to improve policy analysis accuracy, enhance systemic risk assessment, and better represent economic crises and financial market dynamics within macroeconomic predictions.
Agent-based modeling Infographic
 libterm.com
libterm.com