Globe represents the Earth as a three-dimensional model, accurately depicting continents, countries, and oceans, making it an essential tool for geography education and global awareness. Examining a globe enhances Your understanding of spatial relationships and Earth's rotation, providing a realistic perspective that flat maps cannot offer. Explore the rest of this article to discover how globes continue to play a vital role in learning and navigation.
Table of Comparison
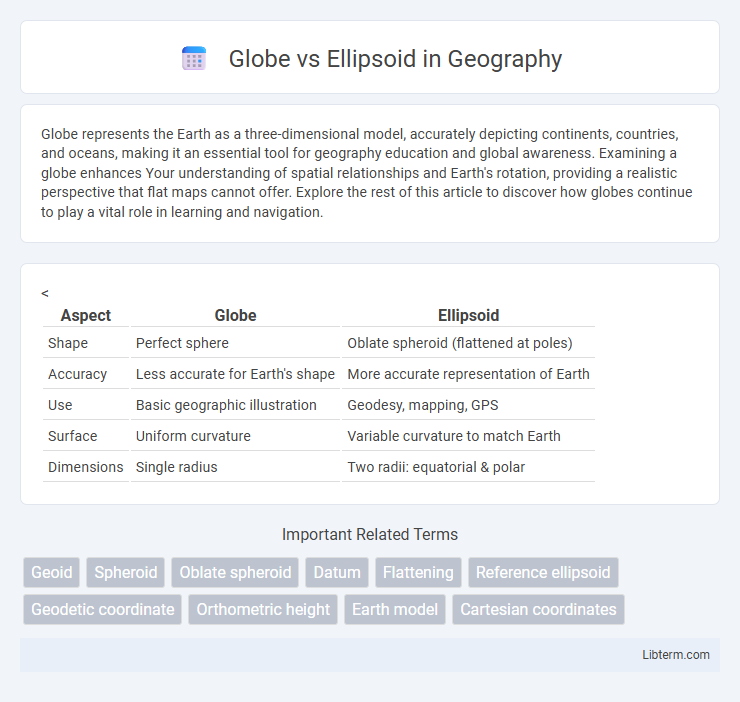
| Aspect | Globe | Ellipsoid |
|---|---|---|
| Shape | Perfect sphere | Oblate spheroid (flattened at poles) |
| Accuracy | Less accurate for Earth's shape | More accurate representation of Earth |
| Use | Basic geographic illustration | Geodesy, mapping, GPS |
| Surface | Uniform curvature | Variable curvature to match Earth |
| Dimensions | Single radius | Two radii: equatorial & polar |
Introduction to Globe and Ellipsoid
A globe is a three-dimensional, spherical model of the Earth that accurately represents continents, oceans, and geographic features without distortion. An ellipsoid, also known as a spheroid, is a mathematically defined surface that approximates the shape of the Earth, accounting for its slightly flattened poles and bulging equator. Globes provide visual and spatial understanding, while ellipsoids serve as fundamental reference surfaces for geodetic calculations and mapping.
Defining a Globe: Shape and Characteristics
A globe is a three-dimensional, spherical model representing Earth with uniform curvature and accurate proportional distances, reflecting its near-perfect round shape. Unlike an ellipsoid, which is mathematically defined with slight flattening at the poles and an equatorial bulge, a globe maintains a consistent radius from its center to any point on its surface. This spherical characteristic makes the globe an ideal tool for visualizing Earth's geography and spatial relationships without distortion.
Understanding the Ellipsoid: Mathematical Formulation
The ellipsoid is a mathematically defined surface generated by rotating an ellipse about its minor axis, characterized by parameters such as the semi-major axis (a) and the semi-minor axis (b), which determine its flattening (f). Its equation in Cartesian coordinates is expressed as (x2 + y2)/a2 + z2/b2 = 1, representing a smooth, closed surface approximating the Earth's shape more accurately than a perfect sphere. This mathematical formulation allows geodesists to model Earth's gravitational field variations and reference surfaces for latitude, longitude, and height measurements with greater precision.
Historical Perspectives: Globe and Ellipsoid in Cartography
Early cartography relied on globes as accurate representations of Earth's spherical shape, essential for navigation and geographic understanding since ancient times. The introduction of ellipsoids in the 18th century refined this approach by accounting for the Earth's equatorial bulge, allowing more precise geodetic measurements and map projections. This shift from globes to ellipsoids marked a pivotal advancement in cartography, enhancing accuracy in global positioning and spatial data analysis.
Physical Differences: Globe vs Ellipsoid
A globe represents the Earth as a perfect sphere with a uniform radius, simplifying shape and distance calculations but lacking precise accuracy due to Earth's polar flattening. An ellipsoid models Earth as a spheroid with an equatorial bulge and flattened poles, providing a more accurate representation of the planet's shape for geodetic and mapping purposes. The physical difference centers on Earth's oblateness, where the ellipsoid's semi-major and semi-minor axes capture the true dimensions, unlike the globe's single-radius approximation.
Applications in Geography and Mapping
Globes provide an accurate three-dimensional representation of Earth, useful for understanding global spatial relationships and visualizing continents, oceans, and climate zones in geography education and thematic mapping. Ellipsoids serve as mathematical models approximating Earth's shape, essential in geodesy and satellite navigation systems like GPS for precise coordinate calculation and map projections. Mapping applications rely on ellipsoids to transform the curved Earth surface onto flat maps, enabling accurate large-scale engineering projects, land surveying, and geographic information systems (GIS).
Accuracy in Representing Earth’s Surface
Ellipsoids provide a mathematically defined surface that closely approximates Earth's shape, enabling higher accuracy in geodetic calculations and map projections compared to globes. Globes represent the Earth as a perfect sphere, which introduces distortions when modeling the slightly flattened poles and equatorial bulge. Using ellipsoids like WGS84 or GRS80 improves precision in GPS positioning, surveying, and geographic information systems by accounting for Earth's actual geoid variations.
Globe and Ellipsoid in Modern GIS
In modern GIS, the globe represents a three-dimensional, spherical Earth model used for accurate distance and spatial relationships, while the ellipsoid provides a mathematically defined, smooth surface approximating the Earth's shape for coordinate system frameworks. Ellipsoids like WGS84 serve as reference surfaces for geodetic calculations, enabling precise positioning and map projections essential in geospatial analysis. The globe offers a realistic visualization for global-scale data, whereas the ellipsoid underpins the geodetic datum critical for GPS and spatial referencing accuracy.
Advantages and Disadvantages: Globe vs Ellipsoid
A globe accurately represents Earth's three-dimensional shape, providing true scale and realistic visualizations but is limited by its lack of portability and detail for large-scale mapping. Ellipsoids offer mathematical simplicity and improved approximation of Earth's shape over spheres, enabling precise geodetic calculations and mapping but can introduce errors in representing regional surface variations due to their smooth, averaged form. Choosing between a globe and an ellipsoid depends on the application's need for realistic visualization versus computational and mapping precision.
Conclusion: Choosing Between Globe and Ellipsoid
Choosing between a globe and an ellipsoid depends on the purpose of accuracy and representation; ellipsoids provide a mathematically precise model of the Earth's shape used in geodesy and GPS systems, while globes offer a visually intuitive, three-dimensional representation valuable for educational and general reference. Ellipsoids account for Earth's flattening at the poles and are essential for precise calculations in mapping and navigation. Globes serve as reliable tools for spatial understanding but lack the detailed accuracy necessary for technical applications.
Globe Infographic
 libterm.com
libterm.com