Understanding calculus concepts can aid in modeling blood glucose levels and insulin dosage in diabetes management. Precise calculations using derivatives and integrals help predict fluctuations and optimize treatment plans. Dive into the rest of this article to discover how calculus plays a crucial role in controlling diabetes effectively.
Table of Comparison
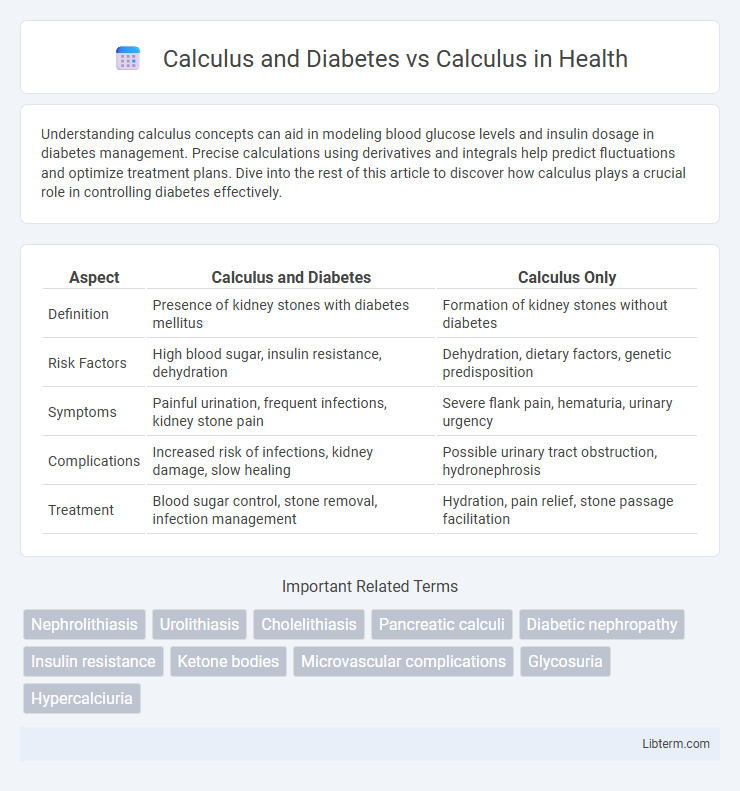
| Aspect | Calculus and Diabetes | Calculus Only |
|---|---|---|
| Definition | Presence of kidney stones with diabetes mellitus | Formation of kidney stones without diabetes |
| Risk Factors | High blood sugar, insulin resistance, dehydration | Dehydration, dietary factors, genetic predisposition |
| Symptoms | Painful urination, frequent infections, kidney stone pain | Severe flank pain, hematuria, urinary urgency |
| Complications | Increased risk of infections, kidney damage, slow healing | Possible urinary tract obstruction, hydronephrosis |
| Treatment | Blood sugar control, stone removal, infection management | Hydration, pain relief, stone passage facilitation |
Introduction to Calculus in Medical Contexts
Introduction to Calculus in medical contexts reveals its critical role in understanding diabetes by modeling glucose-insulin dynamics and predicting blood sugar fluctuations. Differential equations derived from calculus enable precise simulation of insulin response and glucose uptake in diabetic patients, facilitating personalized treatment plans. Utilization of integral calculus assists in analyzing cumulative effects of medication over time, improving diabetes management strategies.
Understanding Diabetes: An Overview
Understanding diabetes requires recognizing its impact on blood sugar regulation and the body's insulin response, which differs fundamentally from mathematical calculus involving rates of change and integration. Diabetes management relies on continuous glucose monitoring and insulin therapy, emphasizing biological processes rather than abstract mathematical concepts found in calculus. The distinction highlights the necessity of specialized medical knowledge to treat diabetes effectively, separate from the theoretical framework of calculus.
The Role of Calculus in Diabetes Management
Calculus plays a critical role in diabetes management by enabling precise modeling of blood glucose levels and insulin dynamics through differential equations. Advanced calculus techniques help predict glucose fluctuations, optimize insulin dosage, and improve artificial pancreas algorithms. Integrating calculus-based models enhances personalized treatment plans and supports continuous glucose monitoring systems for better disease control.
Calculus: Pure Mathematics vs. Medical Applications
Calculus in pure mathematics involves the study of limits, derivatives, integrals, and infinite series to solve abstract problems in continuous change, forming a foundation for advanced mathematical theories. In medical applications, particularly diabetes management, calculus models glucose-insulin dynamics, helping to predict blood sugar levels and optimize insulin dosing. The contrast highlights pure calculus as a theoretical framework, while medical calculus applies these principles to biological systems for practical healthcare solutions.
Mathematical Modeling of Diabetes with Calculus
Mathematical modeling of diabetes leverages calculus to analyze dynamic changes in blood glucose levels, insulin absorption, and pancreatic function over time. Differential equations model insulin-glucose interactions, enabling prediction of glucose regulation and optimization of insulin therapy. Calculus-based models enhance understanding of diabetes progression and support development of personalized treatment plans.
Applications of Calculus in Blood Sugar Monitoring
Calculus plays a crucial role in diabetes management by enabling precise modeling of blood sugar levels through differential equations that describe glucose-insulin dynamics. Continuous glucose monitoring systems utilize integrals to analyze trends and predict future glucose fluctuations, improving insulin dosing accuracy. These applications of calculus enhance personalized treatment plans and support real-time decision-making in diabetes care.
Comparing General Calculus Principles and Diabetes-Specific Calculus
General calculus principles include differentiation, integration, and limits, essential for understanding rates of change and accumulation in various fields. Diabetes-specific calculus applies these concepts to model glucose-insulin dynamics, predict blood sugar levels, and optimize insulin dosing through differential equations. Comparing these reveals how abstract mathematical methods translate into practical healthcare solutions, highlighting the interdisciplinary role of calculus in medical research and diabetes management.
Predictive Analytics: Calculus in Diabetes Risk Assessment
Calculus plays a critical role in predictive analytics by modeling glucose metabolism and insulin response dynamics to assess diabetes risk accurately. Differential equations derived from calculus enable simulation of blood sugar fluctuations, improving early detection and personalized treatment plans. Integration of calculus-based models with patient data enhances precision in forecasting diabetes progression and optimizing intervention strategies.
Integrating Calculus in Diabetes Research and Treatment
Integrating calculus in diabetes research enhances understanding of glucose-insulin dynamics through mathematical modeling of differential equations representing metabolic processes. Calculus enables optimization of insulin dosing by analyzing continuous glucose monitoring data, improving glycemic control and personalized treatment plans. Advanced computational techniques apply integrals and derivatives to predict disease progression and response to therapeutic interventions, driving innovation in diabetes management.
Future Directions: Calculus Innovations in Diabetes Care
Emerging innovations in calculus are revolutionizing diabetes care by enhancing predictive modeling for blood glucose levels and optimizing insulin delivery algorithms. Advanced differential equations and machine learning integrations facilitate personalized treatment plans, improving patient outcomes and reducing hypoglycemic events. Future research focuses on developing real-time calculus-driven analytics that adapt to individual physiological changes, promising more effective and responsive diabetes management systems.
Calculus and Diabetes Infographic
 libterm.com
libterm.com