Algebraic groups combine the structures of algebraic varieties and group theory, providing a rich framework for studying symmetry in geometry and number theory. These groups are defined by polynomial equations over fields, leading to profound connections with Lie groups and representation theory. Explore the rest of the article to understand how algebraic groups influence modern mathematics and your insights into symmetry.
Table of Comparison
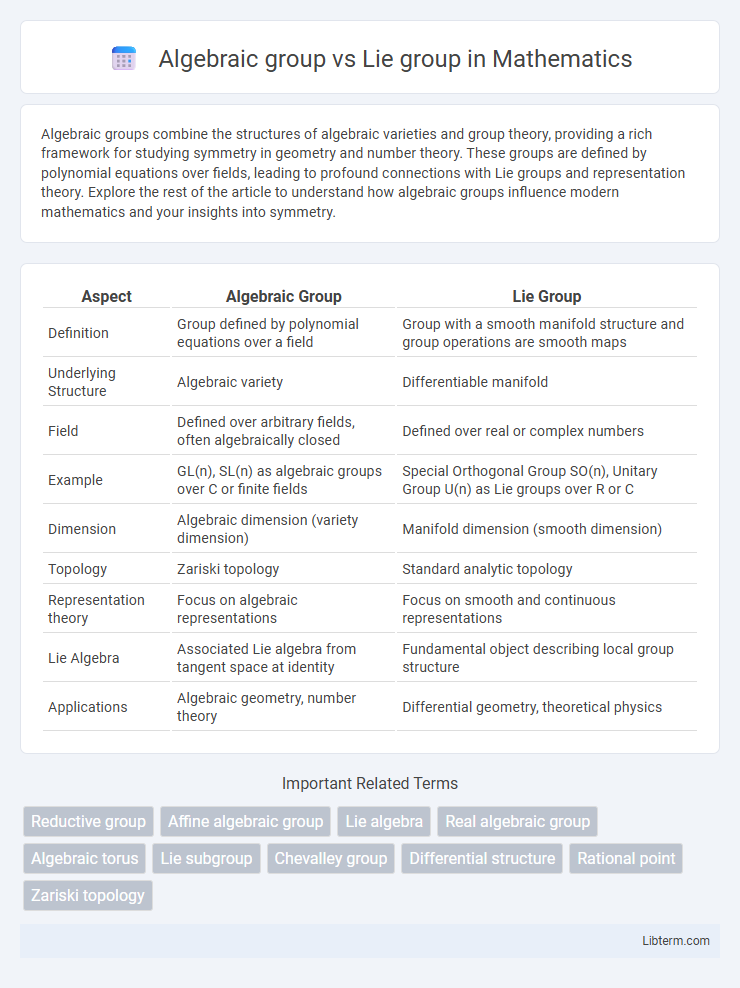
| Aspect | Algebraic Group | Lie Group |
|---|---|---|
| Definition | Group defined by polynomial equations over a field | Group with a smooth manifold structure and group operations are smooth maps |
| Underlying Structure | Algebraic variety | Differentiable manifold |
| Field | Defined over arbitrary fields, often algebraically closed | Defined over real or complex numbers |
| Example | GL(n), SL(n) as algebraic groups over C or finite fields | Special Orthogonal Group SO(n), Unitary Group U(n) as Lie groups over R or C |
| Dimension | Algebraic dimension (variety dimension) | Manifold dimension (smooth dimension) |
| Topology | Zariski topology | Standard analytic topology |
| Representation theory | Focus on algebraic representations | Focus on smooth and continuous representations |
| Lie Algebra | Associated Lie algebra from tangent space at identity | Fundamental object describing local group structure |
| Applications | Algebraic geometry, number theory | Differential geometry, theoretical physics |
Introduction to Algebraic Groups and Lie Groups
Algebraic groups are defined as groups that also have the structure of an algebraic variety, allowing the use of polynomial equations to study their properties, with examples including linear algebraic groups like GL(n). Lie groups, on the other hand, are smooth manifolds equipped with group operations that are differentiable, enabling the application of differential geometry and Lie algebra techniques to analyze their structure. Understanding the fundamental differences between algebraic group theory and Lie group theory highlights the role of algebraic geometry in the former and smooth manifold theory in the latter.
Historical Development of Algebraic and Lie Groups
The historical development of Lie groups began in the late 19th century with Sophus Lie's work on continuous transformation groups to address differential equations, establishing a foundation for the study of smooth manifolds and symmetry. Algebraic groups emerged in the early 20th century through the work of mathematicians like Chevalley and Weil, who explored groups defined by polynomial equations over fields, connecting algebraic geometry to group theory. The interplay between algebraic groups and Lie groups deepened in the mid-20th century, particularly through the study of linear algebraic groups and their Lie algebras, bridging structural and representational aspects of both theories.
Key Definitions: Algebraic Group vs Lie Group
An algebraic group is a group defined by polynomial equations over an algebraically closed field, combining group structure with algebraic variety properties. A Lie group is a smooth manifold equipped with a group structure where the group operations are smooth maps, emphasizing differential and analytic properties. The key distinction lies in algebraic groups being studied via algebraic geometry, while Lie groups are analyzed through differential geometry and smooth analysis.
Structural Differences Between Algebraic and Lie Groups
Algebraic groups are defined by polynomial equations over algebraically closed fields, emphasizing their rigid algebraic structure, while Lie groups are smooth manifolds equipped with group operations that are smooth maps, highlighting their differential geometric nature. Algebraic groups have a Zariski topology that is coarser and less intuitive than the analytic topology on Lie groups, affecting how group actions and representations are studied. The structural difference also lies in their classification: algebraic groups often rely on concepts like root systems and reductive groups, whereas Lie groups focus on Lie algebras and exponential mappings to describe local behavior.
Examples of Algebraic Groups and Lie Groups
Algebraic groups include examples such as the general linear group GL(n), defined over a field, which consists of all invertible nxn matrices with polynomial group operations. Lie groups incorporate examples like the special orthogonal group SO(n), consisting of all nxn real orthogonal matrices with determinant one, forming a smooth manifold structure. Both algebraic groups and Lie groups serve as fundamental objects in understanding symmetries, with algebraic groups emphasizing polynomial structure and Lie groups emphasizing differentiable structure.
Algebraic Groups over Different Fields
Algebraic groups defined over various fields exhibit diverse structural properties, reflecting the underlying field characteristics such as algebraic closure, characteristic, and completeness. Over algebraically closed fields, algebraic groups are closely related to linear algebraic groups described by polynomial equations, while over non-closed fields, Galois cohomology plays a crucial role in classification and understanding of rational points. The behavior of algebraic groups over finite fields contrasts sharply with those over local or global fields, influencing their representation theory and applications in number theory and arithmetic geometry.
Lie Groups and Lie Algebras: The Relationship
Lie groups are smooth manifolds equipped with group structures that enable the study of continuous symmetries, while Lie algebras serve as the tangent space at the identity element of a Lie group, encoding its infinitesimal structure through a bracket operation. The exponential map links Lie algebras to Lie groups, translating algebraic data into local group elements and facilitating analysis of group behavior near the identity. This relationship between Lie groups and Lie algebras forms the foundation for differential geometric methods in representation theory, harmonic analysis, and the classification of continuous symmetry groups.
Applications in Mathematics and Physics
Algebraic groups play a crucial role in number theory and algebraic geometry, particularly in the study of polynomial equations and symmetries of algebraic varieties. Lie groups are fundamental in differential geometry and theoretical physics, especially in modeling continuous symmetries and conservation laws through smooth manifolds and Lie algebras. Both structures underpin gauge theory, representation theory, and particle physics, enabling the classification of elementary particles and the formulation of unified field theories.
Major Theorems Linking Algebraic and Lie Groups
The Major Theorems linking algebraic groups and Lie groups include the Chevalley's Theorem, which constructs complex algebraic groups from Lie algebras, and the Cartier's Theorem, providing equivalence between linear algebraic groups and Lie groups over algebraically closed fields of characteristic zero. The Lie-Kolchin Theorem asserts that any connected solvable linear algebraic group over an algebraically closed field can be triangularized, paralleling results in Lie group theory. These theorems bridge algebraic group structures and Lie group symmetries, enabling transfer of results between algebraic geometry and differential topology.
Summary and Future Directions in Group Theory
Algebraic groups are defined by polynomial equations over algebraic fields and exhibit rigid, well-structured geometric properties, whereas Lie groups possess smooth manifold structures enabling continuous symmetries and differential calculus applications. Recent advancements explore deep interactions between these two classes, emphasizing the role of algebraic groups in arithmetic geometry and Lie groups in theoretical physics. Future directions will likely investigate unified frameworks combining algebraic rigidity with analytic flexibility, fostering breakthroughs in representation theory, number theory, and quantum field theory.
Algebraic group Infographic
 libterm.com
libterm.com