Logical equivalence occurs when two statements always share the same truth value in every possible scenario, making them interchangeable in logical arguments. This concept is fundamental in mathematics, computer science, and philosophy for simplifying expressions and verifying proofs. Explore the rest of the article to understand how logical equivalence can strengthen your reasoning skills.
Table of Comparison
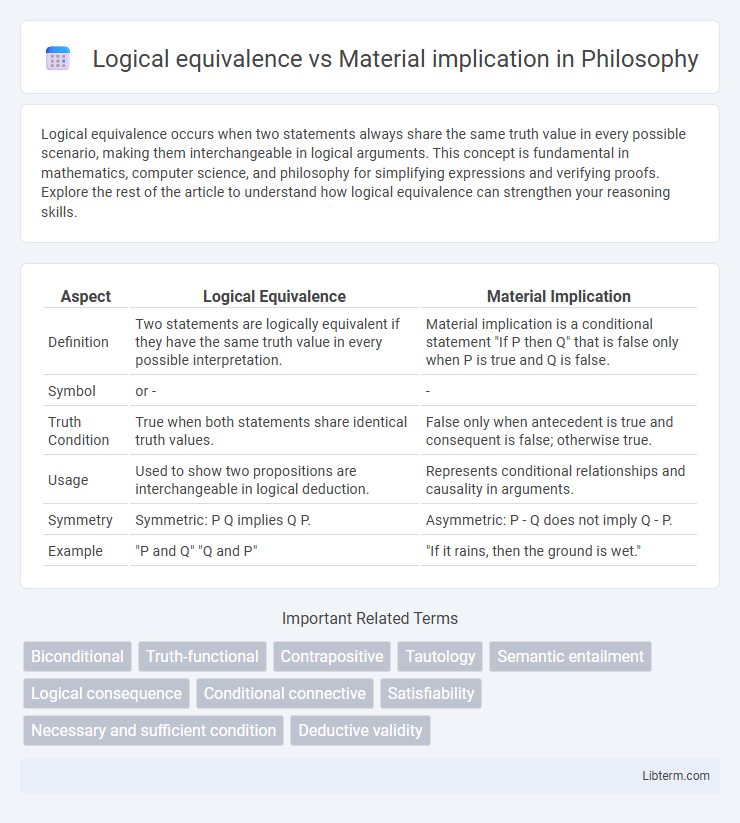
| Aspect | Logical Equivalence | Material Implication |
|---|---|---|
| Definition | Two statements are logically equivalent if they have the same truth value in every possible interpretation. | Material implication is a conditional statement "If P then Q" that is false only when P is true and Q is false. |
| Symbol | or - | - |
| Truth Condition | True when both statements share identical truth values. | False only when antecedent is true and consequent is false; otherwise true. |
| Usage | Used to show two propositions are interchangeable in logical deduction. | Represents conditional relationships and causality in arguments. |
| Symmetry | Symmetric: P Q implies Q P. | Asymmetric: P - Q does not imply Q - P. |
| Example | "P and Q" "Q and P" | "If it rains, then the ground is wet." |
Introduction to Logical Equivalence and Material Implication
Logical equivalence occurs when two statements always share the same truth value across all possible scenarios, indicating they are interchangeable in logical expressions. Material implication, symbolized as \( p \rightarrow q \), represents a conditional statement that is false only when \( p \) is true and \( q \) is false, but true in all other cases. Understanding the distinction between logical equivalence and material implication is crucial for mastering formal logic and constructing valid arguments.
Fundamental Concepts: Logic in Propositional Calculus
Logical equivalence in propositional calculus denotes two statements that always share the same truth value under every possible interpretation, symbolized by a double-sided arrow (-). Material implication represents a conditional relationship where the truth of the antecedent guarantees the truth of the consequent, expressed with a single arrow (-), but it is false only when the antecedent is true and the consequent is false. Understanding the distinction between these fundamental concepts is crucial for manipulating logical formulas, constructing valid arguments, and proving theorems within formal systems.
Defining Logical Equivalence
Logical equivalence is a foundational concept in classical logic where two statements are true in exactly the same scenarios, meaning they have identical truth values across all possible interpretations. This equivalence is symbolized by the biconditional operator (-), indicating that each statement implies the other. In contrast, material implication (-) captures a unidirectional relationship where the truth of one statement guarantees the truth of another but does not require mutual truth across all cases.
Defining Material Implication
Material implication is a logical connective symbolized as "-" that expresses a conditional relationship between two propositions, where the statement "P - Q" is false only when P is true and Q is false. Logical equivalence, denoted by "-", requires both statements to have identical truth values in all scenarios, signifying that P - Q means P and Q imply each other mutually. Material implication captures a one-way conditional connection, whereas logical equivalence ensures bidirectional truth dependency between propositions.
Key Differences between Logical Equivalence and Material Implication
Logical equivalence asserts that two propositions always share the same truth value in every possible scenario, symbolized as \(A \leftrightarrow B\), meaning both imply each other. Material implication, represented by \(A \rightarrow B\), states that if \(A\) is true, then \(B\) must be true, but does not require the reverse. Unlike material implication, logical equivalence ensures bidirectional truth, making it a stronger and more restrictive relation in formal logic.
Truth Tables: Logical Equivalence vs Material Implication
Logical equivalence is true when two statements share identical truth values across all possible scenarios in a truth table, reflecting a bidirectional relationship. Material implication, represented by "if p then q," is false only when the antecedent is true and the consequent false, establishing a unidirectional conditional. Comparing truth tables reveals logical equivalence results in symmetrical truth values, whereas material implication shows asymmetry in truth assignments.
Common Misunderstandings and Pitfalls
Logical equivalence means two statements always have the same truth value, while material implication only requires that if the first statement is true, the second must be true, which often causes confusion. A common pitfall is assuming that !P - Q is equivalent to P Q, ignoring that material implication does not capture the bidirectional guarantee of logical equivalence. Misunderstanding these differences leads to errors in reasoning, especially in formal proofs and programming logic where precise interpretation of "if-then" versus "if and only if" conditions is crucial.
Practical Applications in Mathematics and Computer Science
Logical equivalence enables the replacement of one statement with another without changing truth values, critical in simplifying mathematical proofs and optimizing algorithms in computer science. Material implication expresses conditional statements that model "if-then" scenarios, foundational for constructing logical circuits and decision-making processes in programming. Understanding the distinction improves code correctness verification and enhances automated theorem proving by clearly defining logical relationships.
Symbolic Representation and Notation
Logical equivalence is symbolized as \( A \equiv B \) or \( A \iff B \), indicating that two statements have the same truth value in every possible scenario. Material implication is represented as \( A \rightarrow B \), denoting that if \( A \) is true, then \( B \) must also be true, but does not guarantee \( B \) when \( A \) is false. The distinction in notation highlights that logical equivalence is a bidirectional relationship, while material implication is a unidirectional conditional statement.
Conclusion: Choosing the Right Logical Connector
Logical equivalence ensures two statements always share the same truth value, making it ideal for precise logical deductions, whereas material implication only guarantees that if the antecedent is true, the consequent must be true, without requiring mutual truth alignment. Choosing logical equivalence as a connector is essential when bidirectional truth validation or substitutability in proofs is needed. Material implication suits scenarios involving conditional reasoning, where establishing a cause-effect relation is the primary goal.
Logical equivalence Infographic
 libterm.com
libterm.com