Finitude refers to the inherent limitations and boundaries of existence, emphasizing that all things, including life and resources, are finite. Understanding finitude influences decision-making and encourages mindfulness about how Your time and energy are spent. Explore the rest of the article to delve deeper into the implications of finitude in philosophy and everyday life.
Table of Comparison
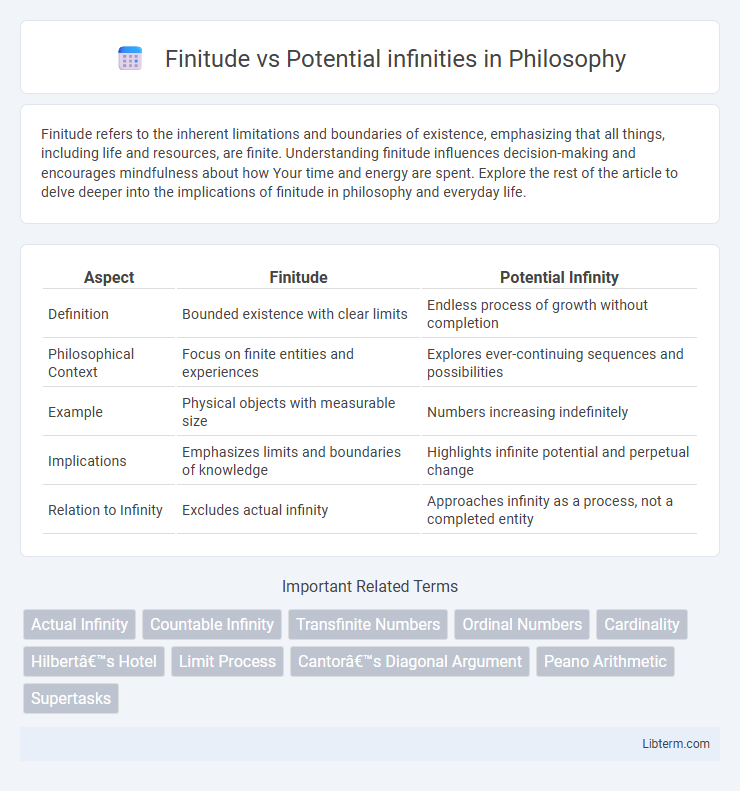
| Aspect | Finitude | Potential Infinity |
|---|---|---|
| Definition | Bounded existence with clear limits | Endless process of growth without completion |
| Philosophical Context | Focus on finite entities and experiences | Explores ever-continuing sequences and possibilities |
| Example | Physical objects with measurable size | Numbers increasing indefinitely |
| Implications | Emphasizes limits and boundaries of knowledge | Highlights infinite potential and perpetual change |
| Relation to Infinity | Excludes actual infinity | Approaches infinity as a process, not a completed entity |
Defining Finitude: Boundaries and Limits
Finitude refers to the inherent boundaries and limits that define the scope of a system, object, or concept, establishing clear endpoints in dimensions such as time, space, or quantity. It contrasts with potential infinities, which represent processes or sequences that can continue indefinitely without an ultimate limit. Understanding finitude is crucial in fields like mathematics, physics, and philosophy, where recognizing finite constraints shapes theoretical models and practical applications.
Understanding Potential Infinity in Mathematics
Potential infinity in mathematics refers to a process that never ends but is never complete, such as counting natural numbers or approaching a limit. Unlike actual infinity, potential infinity is dynamic, representing an unbounded growth or extension rather than a fixed infinite quantity. This concept is fundamental in calculus and analysis, where sequences and functions approach infinite limits without ever fully realizing an infinite value.
Historical Perspectives on Infinity
Historical perspectives on infinity reveal a rich evolution from Aristotle's rejection of actual infinities, favoring potential infinity as a process never completed, to Cantor's revolutionary introduction of actual infinities in set theory, defining different types of infinite cardinalities. Ancient Greek philosophers like Zeno posed paradoxes highlighting the finite versus infinite dichotomy, influencing medieval scholastic debates on the nature of the infinite in theology and cosmology. The shift from finitude to embracing different infinities transformed mathematics, philosophy, and science by providing a framework to rigorously explore infinite structures and processes.
Key Philosophers on Finitude and Infinity
Aristotle established the foundational distinction between actual and potential infinities, arguing that while the actual infinite cannot exist in reality, potential infinity is a process that can continue indefinitely. Immanuel Kant further developed the concept, suggesting human understanding can grasp the idea of infinity only as an idea, not an empirical reality, emphasizing finitude as a limit to human cognition. Georg Cantor revolutionized mathematics by rigorously defining actual infinities through set theory, showing different sizes of infinity and challenging traditional philosophical assumptions about finitude and infinity.
Finitude in Everyday Experience
Finitude in everyday experience manifests through the tangible limitations of time, space, and physical resources that govern human activities and decision-making. People navigate life with an awareness of finite lifespans and constraints, influencing priorities in work, relationships, and personal development. This finite nature shapes perceptions of urgency, value, and the irreversibility of actions within daily contexts.
Potential Infinity in Calculus and Logic
Potential infinity in calculus and logic represents a process that can continue indefinitely without ever reaching completion, such as the infinite sequence of natural numbers or the limit of a function approaching a value. This concept contrasts with actual infinity by emphasizing the unbounded progression within finite steps, critical for understanding limits, series convergence, and inductive reasoning. In formal logic, potential infinity enables the construction of proofs and algorithms that operate over infinite domains without assuming completed infinite totalities.
Paradoxes Arising from Infinite Concepts
Paradoxes arising from infinite concepts highlight the tension between finitude and potential infinities, as seen in Russell's paradox and Zeno's paradoxes, which challenge classical logic and notions of set theory. These paradoxes expose contradictions when assuming the existence of actual infinite collections or divisibility, prompting reevaluations of mathematical infinity and the foundations of calculus. Understanding these issues is critical for advancements in mathematical philosophy and theories of infinite processes.
The Role of Finitude in Scientific Inquiry
Finitude in scientific inquiry imposes inherent limits on observation, experimentation, and data interpretation, necessitating models that operate within finite constraints. This finite perspective drives the development of approximations, empirical methods, and bounded theoretical frameworks that avoid reliance on actual infinite quantities. Recognizing finitude ensures scientific theories remain testable and predictive, maintaining rigor despite the conceptual challenge posed by potential infinities.
Debates: Actual vs. Potential Infinity
The debate between actual and potential infinity centers on whether infinite quantities exist as completed entities or only as processes that can grow indefinitely. Actual infinity refers to a completed, fully realized infinite set, such as the set of all natural numbers, while potential infinity describes an unending process that never attains completion. Philosophers and mathematicians like Georg Cantor champion actual infinity, whereas Aristotle favored potential infinity, influencing foundational perspectives in set theory and calculus.
Implications of Finitude and Infinity in Modern Thought
The implications of finitude and potential infinities in modern thought deeply influence metaphysics, physics, and mathematics by challenging the understanding of existence, time, and space. Finitude emphasizes limits and boundaries, shaping ethical frameworks and existential questions about human experience and mortality. In contrast, potential infinities open avenues for exploring unbounded processes and continuous growth, impacting theories in cosmology and computational models.
Finitude Infographic
 libterm.com
libterm.com