Syllogistic logic, a fundamental branch of classical logic, analyzes arguments structured through categorical propositions involving a major premise, a minor premise, and a conclusion. It allows you to evaluate the validity of deductive reasoning by examining the relationships between different categories or sets. Explore the article to deepen your understanding of syllogistic logic and enhance your reasoning skills.
Table of Comparison
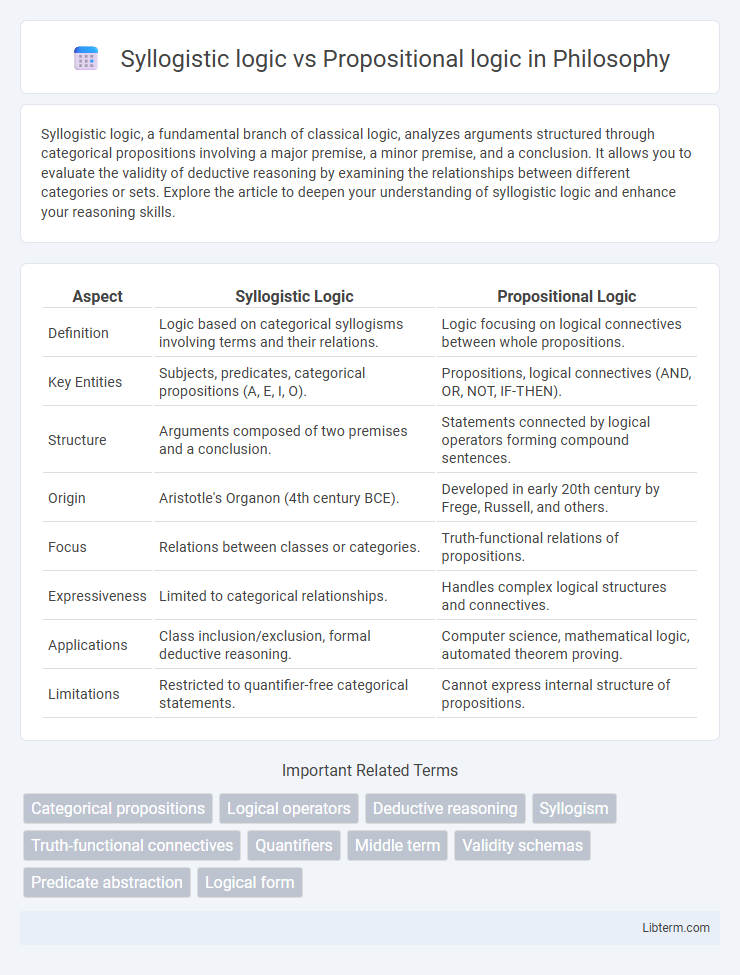
| Aspect | Syllogistic Logic | Propositional Logic |
|---|---|---|
| Definition | Logic based on categorical syllogisms involving terms and their relations. | Logic focusing on logical connectives between whole propositions. |
| Key Entities | Subjects, predicates, categorical propositions (A, E, I, O). | Propositions, logical connectives (AND, OR, NOT, IF-THEN). |
| Structure | Arguments composed of two premises and a conclusion. | Statements connected by logical operators forming compound sentences. |
| Origin | Aristotle's Organon (4th century BCE). | Developed in early 20th century by Frege, Russell, and others. |
| Focus | Relations between classes or categories. | Truth-functional relations of propositions. |
| Expressiveness | Limited to categorical relationships. | Handles complex logical structures and connectives. |
| Applications | Class inclusion/exclusion, formal deductive reasoning. | Computer science, mathematical logic, automated theorem proving. |
| Limitations | Restricted to quantifier-free categorical statements. | Cannot express internal structure of propositions. |
Introduction to Syllogistic and Propositional Logic
Syllogistic logic, originating from Aristotle, analyzes categorical relationships between terms within premises to derive conclusions, focusing on the structure of arguments involving subjects and predicates. Propositional logic, also known as sentential logic, deals with propositions as wholes and uses logical connectives like AND, OR, and NOT to form compound statements and assess their truth values. Understanding syllogistic logic emphasizes term-based inference patterns, whereas propositional logic centers on truth-functional operations and the manipulation of entire propositions.
Historical Background and Origins
Syllogistic logic, originating from Aristotle's works in the 4th century BCE, laid the foundational framework for deductive reasoning through categorical syllogisms involving terms and classes. Propositional logic emerged much later, formalized in the 19th and early 20th centuries by logicians such as George Boole and Gottlob Frege, focusing on the relationships between entire propositions rather than terms within statements. While syllogistic logic dominated medieval and ancient philosophical thought, propositional logic introduced symbolic and algebraic methods that transformed logical analysis into a more rigorous and mathematical discipline.
Core Concepts: Syllogistic Logic Explained
Syllogistic logic centers on categorical propositions and their relationships, using terms like "all," "some," and "none" to form syllogisms composed of a major premise, minor premise, and conclusion. It analyzes logical validity through structured argument forms, such as universal affirmative (A), universal negative (E), particular affirmative (I), and particular negative (O) statements. This core framework contrasts with propositional logic, which emphasizes truth-functional operators and the logical connections between whole propositions rather than term-based relationships.
Fundamentals of Propositional Logic
Propositional logic is a formal system in logic where statements, called propositions, are connected using logical connectives such as AND, OR, NOT, and IMPLIES to form complex expressions. Unlike syllogistic logic, which deals with categorical propositions and their relationships, propositional logic emphasizes the truth values of entire statements and the logical structure of arguments based on these values. The fundamentals of propositional logic include understanding atomic propositions, truth tables, logical equivalences, and rules of inference that enable the derivation of valid conclusions from given premises.
Key Differences Between Syllogistic and Propositional Logic
Syllogistic logic centers on categorical statements and their relationships within deductive reasoning, primarily involving terms like subject and predicate to form syllogisms. Propositional logic, on the other hand, deals with whole propositions connected by logical operators such as AND, OR, and NOT, emphasizing truth-functional relationships. The key difference lies in syllogistic logic analyzing internal structure of categorical terms, while propositional logic focuses on the truth values of compound statements.
Formal Structure and Representation
Syllogistic logic focuses on categorical propositions and their relations within a structured argument form involving premises and a conclusion, primarily using terms like "all," "some," and "none." Propositional logic operates on whole statements represented by propositional variables connected through logical connectives such as "and," "or," "not," and "if-then," emphasizing truth-functional operations. The formal structure of syllogistic logic is based on quantified terms within a logical syllogism, whereas propositional logic uses formulaic expressions and truth tables to analyze logical validity and entailment.
Expressive Power and Limitations
Syllogistic logic, rooted in Aristotelian tradition, excels at expressing categorical relationships between classes but lacks the expressive power to handle complex propositional structures involving multiple logical connectives. Propositional logic, using variables and logical operators like AND, OR, and NOT, offers greater expressive power to represent various truth-functional combinations but cannot directly capture quantified statements or nuanced class-based inferences. Consequently, syllogistic logic is limited in scope and precision compared to propositional logic, which, despite its expressivity, cannot represent internal structure of propositions or quantification inherent in predicate logic.
Typical Applications and Use Cases
Syllogistic logic is primarily used in deductive reasoning and categorical syllogisms, making it ideal for applications in classical philosophy, linguistics, and educational tools that teach formal argument structures. Propositional logic excels in computer science, particularly in designing digital circuits, artificial intelligence algorithms, and automated theorem proving due to its ability to handle complex statements involving logical connectives. Both logics serve distinct roles: syllogistic logic supports reasoning about classes and categories, while propositional logic enables manipulation of truth-functional statements in computational contexts.
Common Errors and Misconceptions
Syllogistic logic often faces errors such as misinterpreting categorical statements and assuming invalid conclusions from incomplete premises, while propositional logic mistakes frequently involve confusing logical connectives or misapplying truth tables. Misconceptions include believing syllogisms guarantee truth if premises appear true, ignoring validity versus soundness, and presuming propositional logic's symbolic form simplifies complex argument content. Both require careful attention to structure and rules to avoid invalid deductions and ensure precise reasoning.
Conclusion: Choosing the Right Logic System
Choosing between syllogistic logic and propositional logic depends on the complexity and type of reasoning required; syllogistic logic excels in categorical statements involving subject-predicate relationships, while propositional logic handles compound statements with logical connectives more efficiently. Propositional logic provides greater flexibility for formal proofs and computational applications, making it ideal for tasks in computer science and mathematical logic. Syllogistic logic remains valuable for understanding classical argument structures and natural language inference where categorical reasoning is predominant.
Syllogistic logic Infographic
 libterm.com
libterm.com