First-order logic formalizes reasoning by using quantifiers and predicates to express statements about objects and their relationships. It serves as a foundational tool in fields like mathematics, computer science, and artificial intelligence for defining and analyzing complex systems. Explore the rest of the article to deepen your understanding of how first-order logic shapes logical frameworks.
Table of Comparison
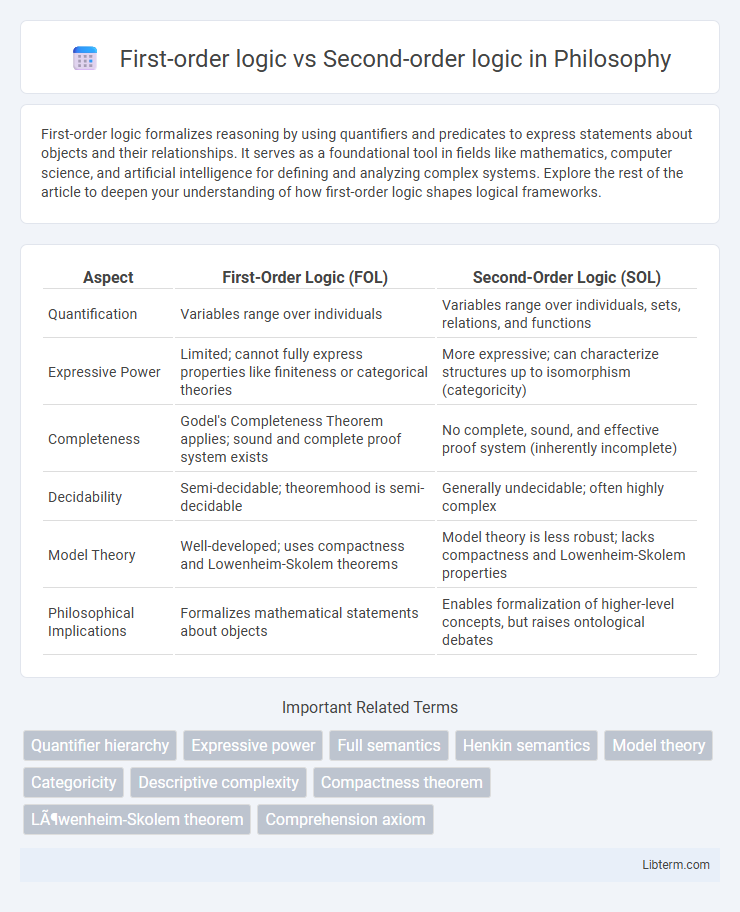
| Aspect | First-Order Logic (FOL) | Second-Order Logic (SOL) |
|---|---|---|
| Quantification | Variables range over individuals | Variables range over individuals, sets, relations, and functions |
| Expressive Power | Limited; cannot fully express properties like finiteness or categorical theories | More expressive; can characterize structures up to isomorphism (categoricity) |
| Completeness | Godel's Completeness Theorem applies; sound and complete proof system exists | No complete, sound, and effective proof system (inherently incomplete) |
| Decidability | Semi-decidable; theoremhood is semi-decidable | Generally undecidable; often highly complex |
| Model Theory | Well-developed; uses compactness and Lowenheim-Skolem theorems | Model theory is less robust; lacks compactness and Lowenheim-Skolem properties |
| Philosophical Implications | Formalizes mathematical statements about objects | Enables formalization of higher-level concepts, but raises ontological debates |
Introduction to First-Order and Second-Order Logic
First-order logic (FOL) allows quantification over individuals, making it powerful for expressing statements about objects in a domain with predicates, functions, and equality. Second-order logic (SOL) extends this by enabling quantification over sets, relations, and functions, thereby increasing its expressive strength significantly. While FOL has a complete and sound proof system, SOL lacks these properties but can formalize a wider range of mathematical concepts.
Foundations and Historical Development
First-order logic, formalized by Gottlob Frege and further developed by Bertrand Russell and Alfred North Whitehead, provides a foundation for mathematics with quantification over individuals but not over predicates or sets, ensuring completeness and compactness theorems. Second-order logic extends quantification to sets and relations, introduced by Charles Sanders Peirce and popularized by Hilbert and Ackermann, offering greater expressive power but losing key properties like completeness and compactness. Historically, first-order logic became the standard tool in formal semantics and foundations of mathematics due to its well-understood meta-theoretical properties, while second-order logic influenced the development of set theory and type theory despite its complexity.
Formal Syntax and Structures
First-order logic utilizes quantifiers over individual variables with a well-defined formal syntax comprising atomic formulas, logical connectives, and quantifiers exclusively ranging over elements of a domain. In contrast, second-order logic extends this syntax by including quantifiers over predicates, functions, and relations, allowing for expressions about properties and sets of elements, thereby increasing its expressive power. Formal structures for first-order logic interpret domain elements and relations, while second-order logic structures require higher-order interpretations, often involving complex set-theoretic or semantic frameworks.
Expressive Power: Comparing Capabilities
First-order logic (FOL) quantifies only over individual elements within a domain, limiting its ability to express properties about sets or relations, whereas second-order logic (SOL) extends this capacity by allowing quantification over sets, relations, and functions, thus enabling richer and more complex expressions. This increased expressive power allows SOL to define concepts like finiteness, continuity, and well-ordering, which cannot be fully captured by FOL. However, the enhanced expressiveness of second-order logic comes at the cost of reduced completeness and decidability compared to first-order logic.
Semantics: Interpretation and Models
First-order logic semantics involve interpretations defined over a domain with assigned meanings to predicates, functions, and constants, ensuring that logical formulas are evaluated based on these fixed assignments. Second-order logic extends this by allowing quantification not only over individual elements but also over relations, functions, and sets, leading to richer models that can capture more complex properties but often at the cost of losing completeness and effective axiomatization. This semantic enhancement enables second-order logic to characterize concepts like categoricity and finiteness, which remain undefinable in first-order logic due to its restricted quantificational scope.
Decidability and Computational Complexity
First-order logic (FOL) is semi-decidable, meaning there exists a procedure that can confirm validity but may not halt for invalid formulas, and its satisfiability problem is semi-decidable with complexities often characterized as recursively enumerable. Second-order logic (SOL) is generally undecidable because it quantifies over predicates and functions, significantly increasing its expressive power and computational complexity beyond any effective algorithmic verification. Complexity classes for SOL reach beyond arithmetical hierarchies, making automated reasoning and satisfiability checks infeasible compared to the more tractable, albeit still complex, decision procedures available for subsets of FOL such as monadic or guarded fragments.
Limitations and Extensions
First-order logic is limited by its inability to quantify over predicates or sets, restricting expressiveness to individual elements and causing challenges in capturing properties like finiteness or completeness. Second-order logic extends expressiveness by allowing quantification over sets and relations, enabling formulations of stronger axioms and more comprehensive mathematical theories. Despite its expressive power, second-order logic often loses desirable meta-logical properties such as completeness and effective axiomatizability, making it less amenable to algorithmic reasoning and proof theory.
Applications in Mathematics and Computer Science
First-order logic is widely applied in automated theorem proving and formal verification due to its decidability and well-established completeness properties. In contrast, second-order logic enables richer expressiveness necessary for defining natural number arithmetic and higher-level mathematical concepts but lacks complete axiomatizability, limiting its direct computational use. Computer science leverages first-order logic for database query languages and logic programming, while second-order logic underpins descriptive complexity theory and advanced specification languages.
Philosophical and Foundational Implications
First-order logic restricts quantification to individuals, enabling complete axiomatizations and effective completeness theorems, which support foundational systems like Peano arithmetic and ZFC set theory. In contrast, second-order logic allows quantification over properties and sets, offering greater expressive power to uniquely characterize structures such as the natural numbers but lacks a complete, effective axiomatization, raising philosophical debates about the nature of mathematical truth and objectivity. This contrast illuminates foundational implications: first-order logic aligns with formalism and mechanized proof systems, while second-order logic resonates with Platonism, reflecting differing views on mathematical existence and epistemology.
Summary and Future Directions
First-order logic, characterized by quantification over individuals, offers decidability and effective model checking, while second-order logic extends this by quantifying over sets and relations, enhancing expressive power at the expense of computational complexity and undecidability. Future research aims to balance expressiveness and tractability by exploring fragments of second-order logic with decidable properties and developing efficient automated reasoning tools. Advances in hybrid logic systems and domain-specific applications promise to leverage the strengths of both first-order and second-order frameworks for improved semantic modeling and verification.
First-order logic Infographic
 libterm.com
libterm.com