Normal blood pressure typically ranges around 120/80 mmHg, indicating a healthy balance between systolic and diastolic pressures. Maintaining this range is crucial for reducing the risk of heart disease and stroke, conditions linked to both high and low blood pressure. Discover effective strategies to keep your blood pressure in check throughout the rest of the article.
Table of Comparison
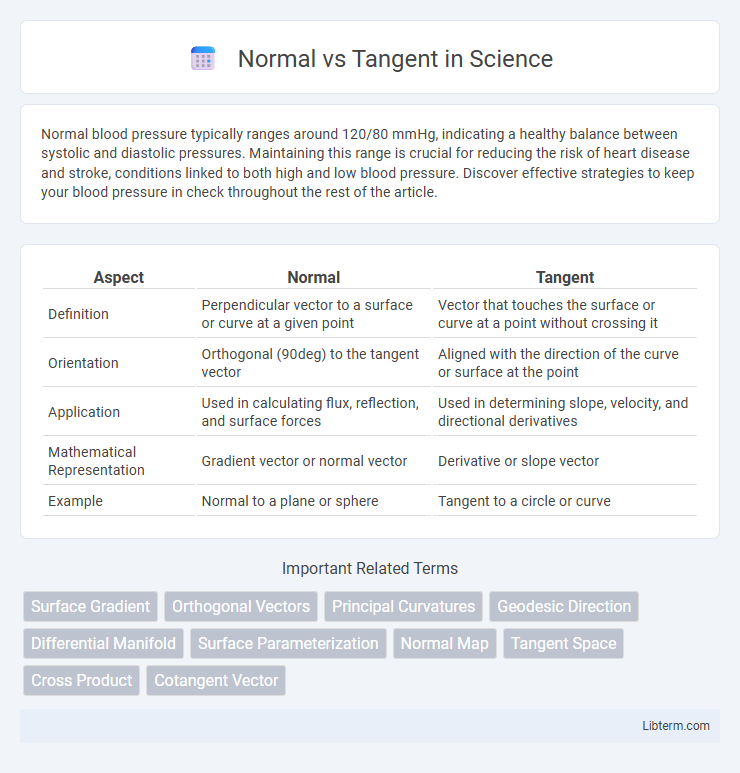
| Aspect | Normal | Tangent |
|---|---|---|
| Definition | Perpendicular vector to a surface or curve at a given point | Vector that touches the surface or curve at a point without crossing it |
| Orientation | Orthogonal (90deg) to the tangent vector | Aligned with the direction of the curve or surface at the point |
| Application | Used in calculating flux, reflection, and surface forces | Used in determining slope, velocity, and directional derivatives |
| Mathematical Representation | Gradient vector or normal vector | Derivative or slope vector |
| Example | Normal to a plane or sphere | Tangent to a circle or curve |
Understanding the Concepts: Normal and Tangent
The concept of a tangent line refers to a straight line that touches a curve at a single point without crossing it, representing the instantaneous direction or slope of the curve at that point. A normal line is perpendicular to the tangent line at the same point of contact and extends outward, representing the direction normal or orthogonal to the curve's surface. Understanding how these lines relate geometrically enhances calculus applications, such as finding slopes, angles of inclination, and optimizing functions through differentiation.
Mathematical Definitions
The normal to a curve at a given point is a line perpendicular to the tangent line, which touches the curve only at that point without crossing it. In calculus, the tangent line represents the instantaneous rate of change or slope of the function at that point, defined by the derivative of the function. The normal line's slope is the negative reciprocal of the tangent's slope, capturing the perpendicular direction in the plane.
Geometric Interpretations
The normal vector represents a direction perpendicular to a surface at a given point, essential in defining surface orientation and calculating reflections or forces in physics and engineering. The tangent vector, conversely, lies along the surface and indicates the direction of the curve or surface at that point, key in determining slopes and directional derivatives. Understanding the geometric interpretations of normal and tangent vectors is crucial in fields like differential geometry, computer graphics, and mechanical design for accurate modeling and analysis.
Properties of Normal Lines
Normal lines are perpendicular to the tangent lines at the point of contact on a curve or surface. They play a crucial role in geometry and calculus, helping to define curvature, surface orientation, and gradient direction. Properties of normal lines include their perpendicularity to tangent vectors and their use in calculating angles of incidence, reflection, and refraction.
Properties of Tangent Lines
Tangent lines touch a curve at exactly one point, exhibiting unique properties such as having a slope equal to the derivative of the function at that point. Unlike normals, which are perpendicular to the tangent, tangent lines provide instantaneous direction and rate of change of the curve. The equation of a tangent line at a point is derived from the point-slope form using the curve's derivative, making it essential in calculus and geometry for analyzing local behavior.
Key Differences Between Normal and Tangent
The key differences between normal and tangent lines lie in their geometric properties: a tangent line touches a curve at exactly one point without crossing it, representing the instantaneous direction of the curve, while a normal line is perpendicular to the tangent at the point of contact, indicating the direction orthogonal to the curve. Tangent lines are defined by the derivative of the function at a specific point, whereas normal lines use the negative reciprocal of the tangent's slope to ensure orthogonality. These distinctions are fundamental in calculus, physics, and geometry for analyzing curves, motion, and forces.
Applications in Calculus and Geometry
Normals are vectors perpendicular to a surface or curve and play a crucial role in optimization problems and defining planes in geometry. Tangents, touching a curve at a single point without crossing it, are essential for determining instantaneous rates of change and slopes in calculus. Applications include calculating gradients using normals for surface orientation and using tangents to analyze function behavior, motion, and curvature in physics and engineering.
Visual Representation and Diagrams
Normal vectors visually appear perpendicular to surfaces, creating right angles that clearly indicate orientation in 3D models and diagrams. Tangent vectors lie flat along curves or surfaces, illustrating direction without crossing the boundary, essential for understanding motion or slope in graphical representations. Diagrams emphasizing normals use right-angle indicators, while tangent representations highlight smooth, continuous lines that follow the object's contour.
Real-world Examples
In computer graphics, normal vectors are essential for determining how light interacts with surfaces, such as calculating shading on a 3D model's curved exterior, while tangent vectors are crucial for texture mapping and handling surface details like wrinkles on a character's skin. Automotive design uses normals to analyze aerodynamic flow over car bodies, whereas tangent vectors help simulate tire contact and traction on road surfaces. In architecture, normals assist in evaluating sunlight angles on building facades, with tangents guiding the placement of surface patterns and materials.
Summary and Conclusion
Normal and tangent lines play crucial roles in geometry and calculus, where the tangent line touches a curve at a single point without crossing it, representing the instantaneous rate of change or slope at that point. The normal line is perpendicular to the tangent line and extends outward from the curve, often used in applications involving reflection, forces, and optimization problems. Understanding the relationship between normal and tangent lines enables more precise analysis of curves and surfaces, facilitating advanced problem-solving in physics, engineering, and mathematics.
Normal Infographic
 libterm.com
libterm.com