Radius is a key measurement in geometry representing the distance from the center of a circle to any point on its circumference, essential for calculating properties such as area and circumference. Understanding how to use the radius enables you to solve various mathematical problems involving circles and spheres efficiently. Explore the rest of the article to master radius-related concepts and applications.
Table of Comparison
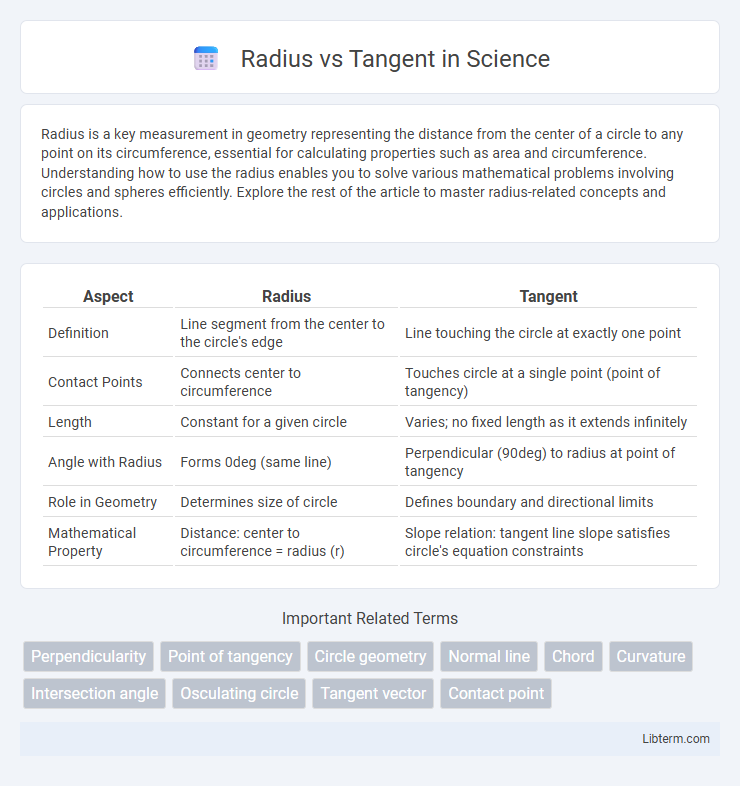
| Aspect | Radius | Tangent |
|---|---|---|
| Definition | Line segment from the center to the circle's edge | Line touching the circle at exactly one point |
| Contact Points | Connects center to circumference | Touches circle at a single point (point of tangency) |
| Length | Constant for a given circle | Varies; no fixed length as it extends infinitely |
| Angle with Radius | Forms 0deg (same line) | Perpendicular (90deg) to radius at point of tangency |
| Role in Geometry | Determines size of circle | Defines boundary and directional limits |
| Mathematical Property | Distance: center to circumference = radius (r) | Slope relation: tangent line slope satisfies circle's equation constraints |
Introduction to Radius and Tangent
Radius is a straight line segment connecting the center of a circle to any point on its circumference, representing the circle's constant distance. Tangent is a straight line that touches the circle at precisely one point, called the point of tangency, without crossing its boundary. Understanding the distinct roles of radius and tangent aids in solving geometric problems related to circles and their properties.
Defining Radius: Key Concepts
The radius is a line segment connecting the center of a circle to any point on its circumference, representing the fixed distance that defines the circle's size. It is a fundamental geometric property used to calculate the circle's area (pr2) and circumference (2pr), where r denotes the radius. Understanding the radius is essential for distinguishing it from a tangent, as the tangent intersects the circle at exactly one point without passing through the center.
Understanding Tangent: Core Principles
A tangent to a circle is a straight line that touches the circle at exactly one point, known as the point of tangency, and is perpendicular to the radius drawn to that point. The core principle of a tangent involves the fact that the radius at the point of tangency forms a 90-degree angle with the tangent line, ensuring no other points of intersection exist between the line and the circle. Understanding this perpendicular relationship helps in solving geometric problems involving circles, such as finding angles, lengths, and areas related to tangents.
Mathematical Relationships Between Radius and Tangent
The radius of a circle is always perpendicular to the tangent line at the point of tangency, forming a 90-degree angle that defines their geometric relationship. If a tangent touches the circle at point P, then the line segment OP, where O is the center, represents the radius and satisfies the condition OP tangent line. The Pythagorean theorem often applies in problems involving the radius and tangent, especially in right triangle solutions related to distances between points outside the circle and tangent lengths.
Visualizing Radius vs Tangent in Geometry
Visualizing the radius and tangent in geometry involves understanding that the radius is the line segment from the center of a circle to any point on its circumference, while the tangent is a line that touches the circle at exactly one point without crossing it. The radius at the point of tangency is perpendicular to the tangent line, highlighting their unique geometric relationship. This perpendicularity is crucial for solving problems involving angles, lengths, and properties of tangents in circle geometry.
Real-World Applications of Radius and Tangent
In real-world applications, the radius plays a crucial role in designing wheels, gears, and circular tracks, determining the curvature and structural integrity of these objects. Tangents are essential in navigation and road design for calculating the exact points where a path meets a curve, ensuring smooth transitions for vehicles. Both radius and tangent concepts are fundamental in engineering fields such as robotics and civil engineering, optimizing motion paths and structural layouts.
Common Mistakes in Differentiating Radius and Tangent
Confusing the radius and tangent often arises from misunderstanding their geometric properties: a radius is a line segment from the circle's center to a point on the circle, while a tangent touches the circle at exactly one point without crossing it. A common mistake is to assume a tangent line passes through the circle's center or to treat the radius as a tangent, which ignores the perpendicularity condition where the tangent is always perpendicular to the radius at the point of contact. Misidentifying these can lead to errors in problems involving circle theorems, derivatives in calculus related to circles, and applications in physics or engineering contexts.
Calculating Tangent Length Using Radius
Calculating the tangent length using the radius involves applying the Pythagorean theorem in a circle where the radius is perpendicular to the tangent at the point of contact. If the distance from the external point to the center of the circle is d and the radius is r, the tangent length t can be found using the formula t = (d2 - r2). This formula is essential in geometry for determining precise tangent lengths when radius and center distance are known.
Radius and Tangent in Engineering and Design
Radius and tangent are fundamental geometric concepts extensively applied in engineering and design, particularly in the creation and analysis of curves and circles. The radius defines the distance from the center of a circle to any point on its circumference, serving as a critical parameter in defining curvature, load distribution, and structural integrity in mechanical components and architectural elements. Tangents, representing lines that touch a curve at exactly one point without intersecting it, are crucial for determining directional slopes, optimizing aerodynamic surfaces, and ensuring precise machining paths in CNC processes.
Conclusion: Choosing Between Radius and Tangent
Choosing between radius and tangent depends on the geometric context and the desired properties in applications such as construction, design, or mathematics. Radius provides direct measurement from the circle's center to any point on the circumference, essential for defining circle size and area calculations. Tangent, being a line that touches the circle at exactly one point without crossing it, is crucial for understanding circle boundaries, slope, and angles, especially in calculus and physics problems.
Radius Infographic
 libterm.com
libterm.com