Matrix technology revolutionizes data organization and complex problem-solving by enabling efficient computation through rows and columns. Understanding its applications in computer graphics, machine learning, and scientific simulations can enhance your ability to leverage data-driven insights. Explore the rest of the article to discover practical uses and advanced concepts behind matrix operations.
Table of Comparison
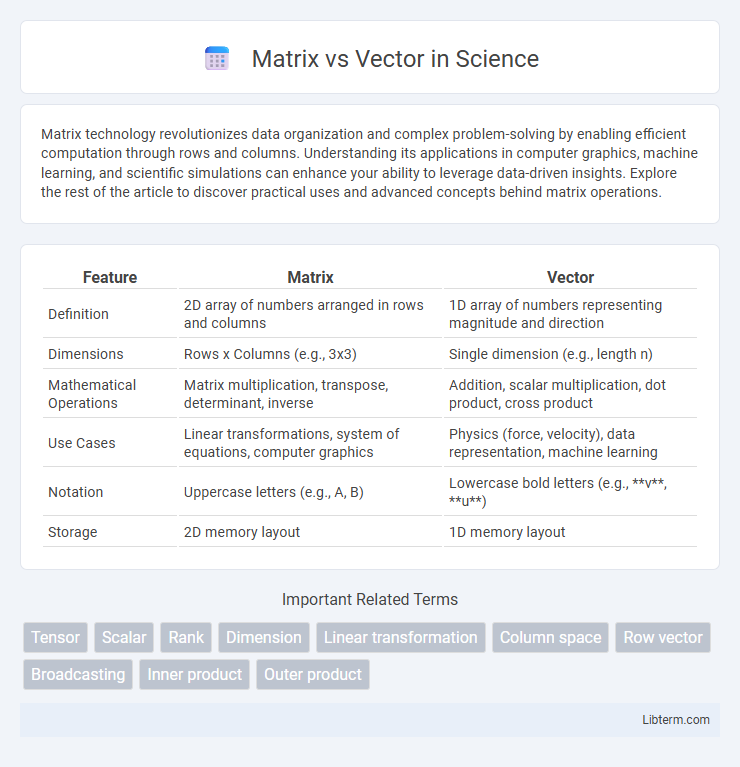
| Feature | Matrix | Vector |
|---|---|---|
| Definition | 2D array of numbers arranged in rows and columns | 1D array of numbers representing magnitude and direction |
| Dimensions | Rows x Columns (e.g., 3x3) | Single dimension (e.g., length n) |
| Mathematical Operations | Matrix multiplication, transpose, determinant, inverse | Addition, scalar multiplication, dot product, cross product |
| Use Cases | Linear transformations, system of equations, computer graphics | Physics (force, velocity), data representation, machine learning |
| Notation | Uppercase letters (e.g., A, B) | Lowercase bold letters (e.g., v, u) |
| Storage | 2D memory layout | 1D memory layout |
Introduction to Matrix and Vector
Matrices represent rectangular arrays of numbers arranged in rows and columns, facilitating complex linear transformations and data representation in fields like computer graphics, physics, and engineering. Vectors are ordered lists of numbers, often representing points or directions in space, and are fundamental to vector algebra and geometry. Both matrices and vectors form the core components of linear algebra, enabling operations such as matrix multiplication, vector addition, and scalar products.
Definitions: What is a Matrix? What is a Vector?
A matrix is a rectangular array of numbers arranged in rows and columns, used to represent linear transformations and organize data in multiple dimensions. A vector is a one-dimensional array of numbers that represents a magnitude and direction in a specific space, often serving as a fundamental building block for matrices. Matrices can be composed of multiple vectors, with vectors functioning as matrix rows or columns within mathematical computations.
Key Differences Between Matrices and Vectors
Matrices are two-dimensional arrays of numbers organized in rows and columns, used to represent linear transformations and systems of equations, whereas vectors are one-dimensional arrays representing magnitude and direction in space. Key differences include dimensionality, with matrices having both rows and columns and vectors having only a single dimension, and operations, where matrices support multiplication with vectors and other matrices, while vectors primarily support operations like dot product and cross product. Understanding these distinctions is crucial in fields like linear algebra, machine learning, and computer graphics for efficient data representation and manipulation.
Structure and Dimensions: Matrix vs Vector
A matrix is a two-dimensional array consisting of rows and columns, allowing it to represent data in a grid-like structure with dimensions m x n, where m is the number of rows and n is the number of columns. In contrast, a vector is a one-dimensional array that can be either a row vector or a column vector, having a single dimension with length n or m respectively. The structural difference enables matrices to perform complex linear transformations and represent systems of equations, while vectors primarily represent points or directions in space.
Operations: How Matrices and Vectors Interact
Matrix-vector multiplication involves multiplying each row of the matrix by the vector, resulting in a new vector that is a linear combination of the matrix's columns; this operation is fundamental in transforming coordinate systems and solving linear equations. Dot products calculate the scalar projection of one vector onto another, while cross products produce a vector orthogonal to the input vectors in three-dimensional space. Vector addition and scalar multiplication operate element-wise, whereas matrices enable more complex transformations such as rotations, scalings, and shearing through matrix multiplication.
Applications in Mathematics and Science
Matrices and vectors are fundamental tools in mathematics and science, with matrices representing linear transformations or systems of equations, and vectors expressing quantities with both magnitude and direction. In physics, vectors describe forces, velocities, and fields, while matrices are essential in quantum mechanics for state transformations and in computer graphics for spatial rotations and scaling. Additionally, in data science and engineering, vectors store multidimensional data points, whereas matrices handle complex operations like solving linear systems and performing eigenvalue decomposition.
Matrix and Vector in Machine Learning
Matrices and vectors form the foundation of machine learning, representing data and operations within algorithms. A matrix, a two-dimensional array of numbers, organizes datasets, weights, and transformations, enabling complex computations such as linear regression and neural network training. Vectors serve as one-dimensional arrays that represent features, parameters, or activations, facilitating operations like dot products and gradient calculations essential for model optimization.
Performance and Efficiency Considerations
Matrix operations often demand significantly more computational resources and memory compared to vector operations, impacting performance in large-scale applications. Vectorized computations leverage hardware acceleration and parallel processing, leading to faster execution and reduced latency in machine learning and numerical algorithms. Efficient data handling strategies, such as sparse matrix representations and optimized linear algebra libraries, can mitigate performance overhead in matrix computations.
Common Use Cases and Examples
Matrices are widely used in computer graphics for transformations such as rotation, scaling, and translation, while vectors represent points or directions in space. In scientific computing, matrices solve systems of linear equations, whereas vectors often describe magnitudes and directions in physics simulations. Machine learning algorithms utilize matrices to store datasets and weight parameters, with vectors representing feature inputs or outputs in predictive models.
Summary: Choosing Between Matrix and Vector
Matrices are ideal for representing and manipulating multi-dimensional data such as images, graphs, and systems of equations, providing a structured way to perform linear transformations. Vectors are preferable for one-dimensional data like feature sets, coordinates, or time series, offering simplicity and efficiency in computation. Selecting between a matrix and vector depends on data dimensionality, operation requirements, and context-specific processing needs.
Matrix Infographic
 libterm.com
libterm.com