Rabin-Karp is an efficient string searching algorithm that uses hashing to find patterns within text, enabling rapid detection of substring matches. Its ability to quickly compare hash values reduces the time complexity for multiple pattern searches, making it ideal for applications like plagiarism detection and data retrieval. Explore the rest of the article to understand how Rabin-Karp can optimize your text search tasks.
Table of Comparison
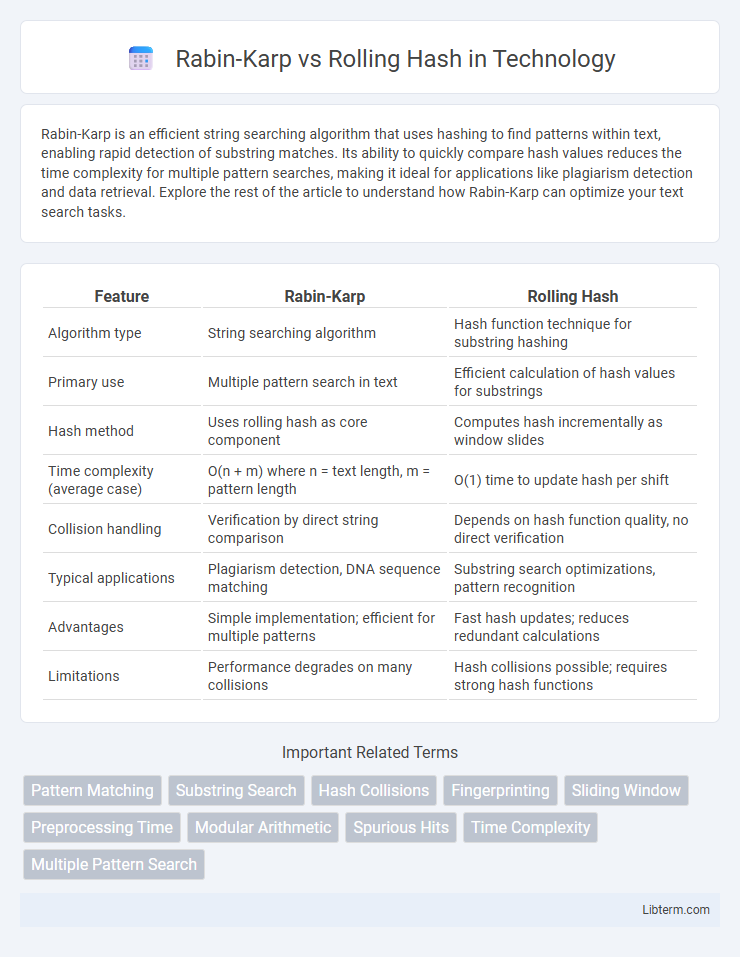
| Feature | Rabin-Karp | Rolling Hash |
|---|---|---|
| Algorithm type | String searching algorithm | Hash function technique for substring hashing |
| Primary use | Multiple pattern search in text | Efficient calculation of hash values for substrings |
| Hash method | Uses rolling hash as core component | Computes hash incrementally as window slides |
| Time complexity (average case) | O(n + m) where n = text length, m = pattern length | O(1) time to update hash per shift |
| Collision handling | Verification by direct string comparison | Depends on hash function quality, no direct verification |
| Typical applications | Plagiarism detection, DNA sequence matching | Substring search optimizations, pattern recognition |
| Advantages | Simple implementation; efficient for multiple patterns | Fast hash updates; reduces redundant calculations |
| Limitations | Performance degrades on many collisions | Hash collisions possible; requires strong hash functions |
Introduction to Rabin-Karp and Rolling Hash
Rabin-Karp is a string searching algorithm that uses hashing to find patterns efficiently by comparing hash values rather than characters directly. The Rolling Hash technique enables constant-time hash computation for sliding windows in text, facilitating fast updates of the hash value as the search window moves. Combining Rabin-Karp with a Rolling Hash allows for rapid pattern matching with reduced computational overhead in large texts.
Core Concepts and Definitions
Rabin-Karp is a string-searching algorithm that uses hashing to efficiently find substrings within a text by comparing hash values rather than characters directly. The core concept involves generating a rolling hash, which updates the hash value in constant time as the search window slides over the text, enabling fast substring matching. The rolling hash function is essential for both Rabin-Karp and other algorithms, providing a mechanism to compute hash values for consecutive substrings with minimal recomputation.
Algorithmic Workflow Comparison
The Rabin-Karp algorithm utilizes a rolling hash technique to efficiently find pattern matches by computing hash values for substrings of the text and comparing them against the pattern's hash. Its algorithmic workflow involves sliding a fixed-length window over the text, updating the hash in constant time by removing the leading character and adding the trailing character, enabling rapid pattern detection. The rolling hash serves as the core component of Rabin-Karp, reducing computational complexity and minimizing direct string comparisons during substring matching.
Hash Function Design and Optimization
Rabin-Karp algorithm relies heavily on an efficient rolling hash function to achieve average-case linear time complexity for substring search by updating the hash value incrementally as the search window moves. Optimal hash function design in Rabin-Karp minimizes collisions by using a large prime modulus and a carefully chosen base, ensuring uniform distribution of hash values for strings of varying lengths. Rolling hash optimization focuses on reducing computational overhead through modular arithmetic techniques and precomputed powers of the base to speed up the hash recalculations during pattern matching.
Pattern Matching Efficiency
Rabin-Karp algorithm utilizes a rolling hash technique to achieve efficient pattern matching by computing hash values for the pattern and substrings of the text, allowing for constant-time comparison of the hashed values rather than direct string comparison. The rolling hash function updates the hash value in O(1) time as the window slides over the text, significantly improving the average-case time complexity to O(n + m) for pattern matching, where n is the length of the text and m is the length of the pattern. While Rabin-Karp can suffer from hash collisions, leading to occasional false positives and extra verification steps, its efficiency in handling multiple pattern searches and large alphabets makes it superior to naive string matching algorithms in many practical scenarios.
Collision Handling Strategies
Rabin-Karp algorithm uses a rolling hash function to efficiently search for patterns in a text, but it requires robust collision handling strategies to avoid false positives caused by hash value matches. Common collision handling methods include verifying the actual substring after a hash match and using multiple hash functions to reduce collision probability. Rolling hash techniques enhance Rabin-Karp's performance by allowing constant-time hash updates, but effective collision resolution remains crucial for accuracy in pattern matching.
Time and Space Complexity Analysis
Rabin-Karp algorithm employs a rolling hash technique to achieve average-case time complexity of O(n + m) for string matching, where n is the length of the text and m is the pattern length, but its worst-case time complexity can degrade to O(nm) due to hash collisions. The rolling hash method efficiently maintains hash values in constant time O(1) for each substring, resulting in overall linear scanning without recomputing hashes from scratch. Space complexity for Rabin-Karp is O(1) beyond the input storage, primarily requiring constant extra space to store hash values, making it highly efficient in memory usage.
Practical Applications and Use Cases
Rabin-Karp algorithm leverages rolling hash to efficiently detect pattern matches in large texts, making it ideal for plagiarism detection and DNA sequence analysis. Rolling hash enables quick hash recalculations as the search window moves, optimizing substring searches in real-time systems like network intrusion detection. Applications in text editors and database query matching benefit from Rabin-Karp's ability to handle multiple pattern searches with reduced computational complexity.
Strengths and Limitations
The Rabin-Karp algorithm employs a rolling hash technique to efficiently find patterns in strings, making it highly effective for multiple pattern searches due to its average-case linear time complexity. Its strength lies in the rapid calculation of hash values, enabling quick substring comparisons and reducing redundant computations. However, the method's performance can degrade to O(nm) in the worst case because of hash collisions, and it requires careful selection of hash functions to minimize false positives and maintain accuracy.
Choosing the Right Approach
Choosing the right approach between Rabin-Karp and Rolling Hash depends on the specific application requirements, such as pattern length, text size, and collision tolerance. Rabin-Karp leverages rolling hash techniques for efficient multiple pattern searches but may suffer from hash collisions requiring verification steps. Optimizing performance involves selecting a robust rolling hash function and hash size to minimize collisions while balancing runtime and memory constraints.
Rabin-Karp Infographic
 libterm.com
libterm.com