B-Tree is a self-balancing tree data structure that maintains sorted data and allows efficient insertion, deletion, and search operations, widely used in databases and file systems. Its design minimizes disk reads, making it suitable for storage systems where accessing data in blocks is essential. Explore the rest of the article to understand how B-Trees optimize data management and improve your system's performance.
Table of Comparison
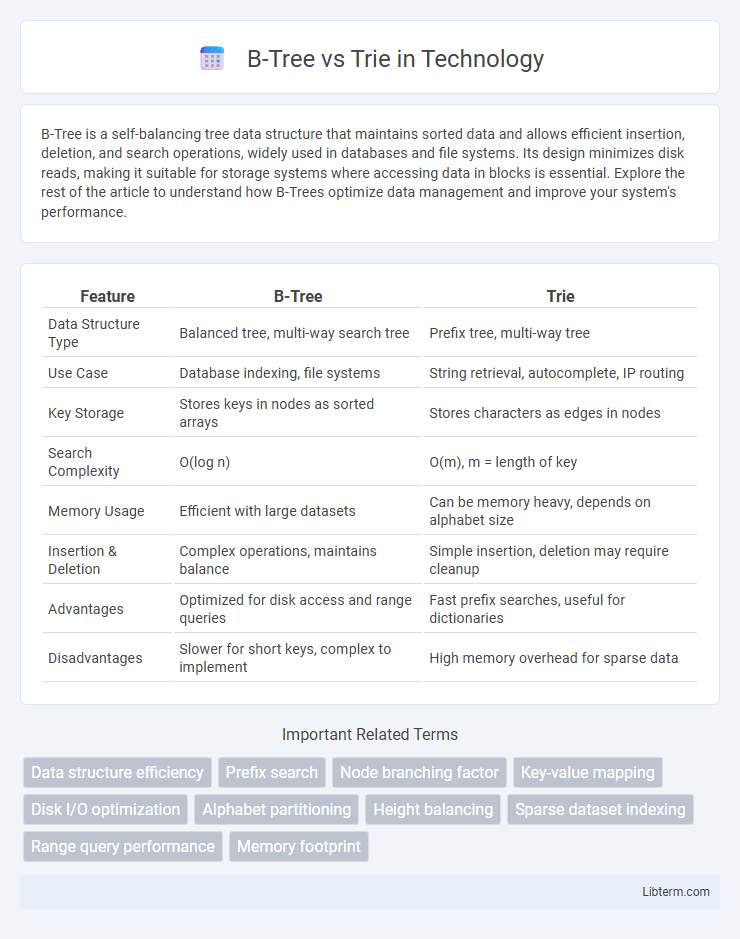
| Feature | B-Tree | Trie |
|---|---|---|
| Data Structure Type | Balanced tree, multi-way search tree | Prefix tree, multi-way tree |
| Use Case | Database indexing, file systems | String retrieval, autocomplete, IP routing |
| Key Storage | Stores keys in nodes as sorted arrays | Stores characters as edges in nodes |
| Search Complexity | O(log n) | O(m), m = length of key |
| Memory Usage | Efficient with large datasets | Can be memory heavy, depends on alphabet size |
| Insertion & Deletion | Complex operations, maintains balance | Simple insertion, deletion may require cleanup |
| Advantages | Optimized for disk access and range queries | Fast prefix searches, useful for dictionaries |
| Disadvantages | Slower for short keys, complex to implement | High memory overhead for sparse data |
Introduction to B-Tree and Trie
B-Trees are balanced tree data structures widely used in databases and file systems to store and retrieve sorted data efficiently, supporting logarithmic time complexity for search, insert, and delete operations. Tries, or prefix trees, specialize in handling dynamic sets of strings by storing common prefixes in shared nodes, enabling fast retrieval of keys, often used in applications like autocomplete and spell checking. While B-Trees optimize data storage on disk and handle large datasets with flexible node sizes, Tries excel in prefix-based searches and are particularly effective for exact or prefix matching of hierarchical data such as words or IP addresses.
Core Concepts and Data Structures
B-Trees are balanced tree data structures optimized for systems that read and write large blocks of data, organizing keys in sorted order with multiple children per node to ensure logarithmic search, insert, and delete operations. Tries, also known as prefix trees, represent keys as paths from the root to leaves, efficiently storing and searching strings by breaking them down into characters or bits, often used for autocomplete and dictionary implementations. While B-Trees excel in range queries and disk-based storage with nodes containing multiple keys, Tries provide fast lookups for exact and prefix matches with space complexity depending on the alphabet size.
Storage Efficiency Comparison
B-Trees optimize storage by storing keys in sorted order with minimal redundancy, using nodes that hold multiple keys and pointers, which reduces disk I/O and maximizes space utilization across large datasets. Tries store keys by breaking them into individual characters, resulting in high memory overhead due to many pointers and often sparse node structures, especially when keys have long prefixes or limited commonality. Consequently, B-Trees provide superior storage efficiency in scenarios with large-scale data and disk storage, while Tries excel in fast prefix-based retrieval but at the cost of increased memory consumption.
Search Operation Performance
B-Trees maintain balanced multi-way structures ideal for disk-based storage, providing logarithmic search time O(log n) by reducing tree height and minimizing I/O operations. Tries, built on prefix-based node branching, offer faster search performance with time complexity O(m), where m is the length of the search key, especially beneficial for prefix and exact-match queries. While B-Trees excel in range queries and large datasets on disk, Tries outperform in memory-based applications with frequent string lookups and autocomplete functionality.
Insert and Delete Operations
B-Trees excel in insert and delete operations by maintaining balanced nodes through splitting and merging, ensuring logarithmic time complexity suitable for large datasets and external storage. Tries enable fast insert and delete operations by directly accessing nodes based on key prefixes, providing efficient performance for string keys at the cost of higher memory usage. B-Trees optimize disk-based databases with minimal rebalancing needed during modifications, while Tries offer superior speed in applications demanding prefix searches and dynamic key manipulation.
Use Cases and Applications
B-Trees excel in database indexing and file systems where balanced tree structures enable efficient range queries and sorted data retrieval. Tries are ideal for prefix-based searches, autocomplete systems, and IP routing tables due to their character-by-character storage enabling fast lookups. Both data structures optimize search performance but serve distinct purposes: B-Trees manage large-scale disk-based storage efficiently, while Tries are preferred for in-memory operations involving string keys.
Handling Large Datasets
B-Trees efficiently handle large datasets by maintaining balanced nodes that optimize disk reads and write operations, making them ideal for database indexing and file systems. Tries excel in managing large collections of strings by enabling fast prefix-based searches with time complexity proportional to the key length, but they often require more memory due to node storage overhead. When scaling, B-Trees offer better space efficiency and disk performance, whereas tries provide faster retrieval for string keys at the cost of increased memory usage.
Memory Usage Analysis
B-Trees optimize memory usage by storing keys and pointers in nodes, allowing balanced tree height and efficient disk access, making them ideal for large datasets on disk-based systems. Tries consume more memory due to storing each character of keys in separate nodes and maintaining multiple child pointers, resulting in sparse structures especially with large alphabets. Memory usage of B-Trees scales with the number of keys and node size, whereas Tries' memory grows exponentially with key length and alphabet size, making B-Trees more memory-efficient for large datasets with longer keys.
Scalability and Speed
B-Trees offer scalable performance in database indexing by maintaining balanced tree height, enabling logarithmic time complexity for search, insert, and delete operations even with large datasets. Tries provide superior speed for prefix-based searches due to direct character indexing but can consume more memory, impacting scalability when handling extensive or sparse alphabets. Choosing between B-Trees and Tries depends on application requirements for memory efficiency versus rapid prefix querying in large-scale environments.
Pros and Cons of B-Tree vs Trie
B-Tree offers efficient storage and retrieval for large datasets with balanced multi-way search trees, providing logarithmic search, insertion, and deletion times ideal for databases and file systems. Tries excel at prefix-based queries and provide faster search times for strings by exploiting common prefixes, but they consume more memory due to node overhead and sparse branches. B-Trees optimize disk read/writes with high branching factors, making them scalable for secondary storage, while tries are more suited for in-memory applications requiring quick autocomplete and dictionary lookups.
B-Tree Infographic
 libterm.com
libterm.com