Value at Risk (VaR) measures the potential financial loss in a portfolio over a specific time frame, under normal market conditions. It helps you quantify risk by estimating the maximum expected loss with a given confidence level, guiding investment and risk management decisions. Explore the rest of the article to understand how VaR can protect your assets and improve your financial strategy.
Table of Comparison
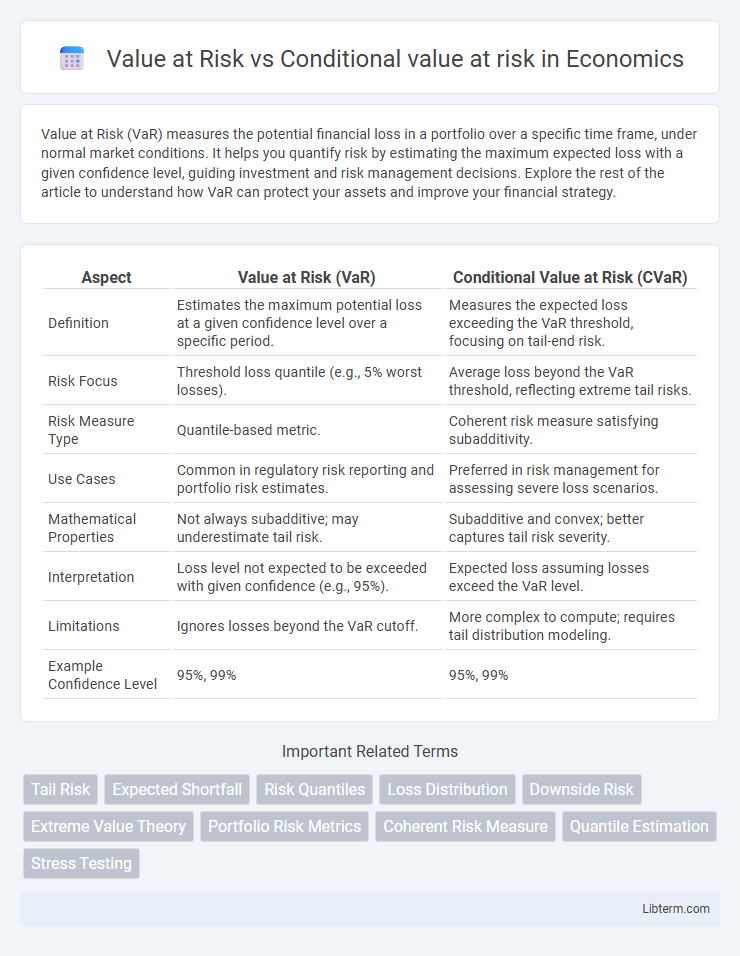
| Aspect | Value at Risk (VaR) | Conditional Value at Risk (CVaR) |
|---|---|---|
| Definition | Estimates the maximum potential loss at a given confidence level over a specific period. | Measures the expected loss exceeding the VaR threshold, focusing on tail-end risk. |
| Risk Focus | Threshold loss quantile (e.g., 5% worst losses). | Average loss beyond the VaR threshold, reflecting extreme tail risks. |
| Risk Measure Type | Quantile-based metric. | Coherent risk measure satisfying subadditivity. |
| Use Cases | Common in regulatory risk reporting and portfolio risk estimates. | Preferred in risk management for assessing severe loss scenarios. |
| Mathematical Properties | Not always subadditive; may underestimate tail risk. | Subadditive and convex; better captures tail risk severity. |
| Interpretation | Loss level not expected to be exceeded with given confidence (e.g., 95%). | Expected loss assuming losses exceed the VaR level. |
| Limitations | Ignores losses beyond the VaR cutoff. | More complex to compute; requires tail distribution modeling. |
| Example Confidence Level | 95%, 99% | 95%, 99% |
Introduction to Value at Risk (VaR) and Conditional Value at Risk (CVaR)
Value at Risk (VaR) quantifies the maximum expected loss over a specified time horizon at a given confidence level, serving as a critical risk metric in finance. Conditional Value at Risk (CVaR), also known as Expected Shortfall, extends VaR by measuring the average loss exceeding the VaR threshold, providing a more comprehensive assessment of tail risk. Both metrics are essential for portfolio risk management, with CVaR offering enhanced sensitivity to extreme loss scenarios beyond the VaR cutoff.
Defining Value at Risk (VaR)
Value at Risk (VaR) estimates the maximum potential loss of a portfolio over a specified time frame at a given confidence level, such as 95% or 99%. It quantifies risk by predicting the worst expected loss under normal market conditions, making it a fundamental metric in financial risk management. Unlike Conditional Value at Risk (CVaR), which considers the tail losses beyond the VaR threshold, VaR focuses solely on the cutoff point without assessing the severity of losses beyond that limit.
Defining Conditional Value at Risk (CVaR)
Conditional Value at Risk (CVaR) measures the expected loss that exceeds the Value at Risk (VaR) threshold, providing a more comprehensive assessment of tail risk in financial portfolios. Unlike VaR, which estimates the maximum potential loss at a given confidence level, CVaR quantifies the average severity of losses beyond that level, enhancing risk management strategies. This makes CVaR particularly valuable for institutions aiming to minimize extreme losses under uncertain market conditions.
Key Differences Between VaR and CVaR
Value at Risk (VaR) estimates the maximum potential loss over a specified time frame at a given confidence level, while Conditional Value at Risk (CVaR) measures the expected loss exceeding the VaR threshold, providing a more comprehensive risk assessment. VaR is limited by its inability to account for the magnitude of losses beyond the threshold, whereas CVaR captures tail risk and is sensitive to the shape of the loss distribution. CVaR is preferred in financial risk management when analyzing extreme losses and improving portfolio optimization under stress scenarios.
Mathematical Formulations of VaR and CVaR
Value at Risk (VaR) quantifies the maximum potential loss over a specified time horizon at a given confidence level a, mathematically defined as the a-quantile of the loss distribution: VaR_a = inf{l R : P(L <= l) >= a}. Conditional Value at Risk (CVaR), also known as Expected Shortfall, represents the expected loss exceeding the VaR threshold, formulated as CVaR_a = E[L | L >= VaR_a], capturing tail risk beyond the VaR cutoff. Both metrics are pivotal in risk management, with CVaR offering a coherent risk measure addressing the shortcomings of VaR regarding tail loss sensitivity.
Practical Applications in Risk Management
Value at Risk (VaR) estimates the maximum potential loss over a specific time frame at a given confidence level, widely used for regulatory capital calculation and daily risk monitoring in financial institutions. Conditional Value at Risk (CVaR), or Expected Shortfall, provides the average loss exceeding the VaR threshold, offering a more comprehensive risk assessment for tail events in portfolio optimization and stress testing. Risk managers prefer CVaR when addressing extreme market scenarios, as it captures the severity of losses beyond VaR, enhancing decision-making in capital allocation and contingency planning.
Advantages and Limitations of VaR
Value at Risk (VaR) offers a clear, quantifiable metric for potential losses over a specific time frame at a given confidence level, making it widely used for risk management and regulatory purposes. Its advantages include simplicity, ease of communication, and compatibility with various asset classes, but VaR's limitations lie in its inability to capture extreme tail risks and its lack of subadditivity, which can underestimate aggregate portfolio risk. Conditional Value at Risk (CVaR), also known as Expected Shortfall, addresses these limitations by considering the expected losses beyond the VaR threshold, providing a more coherent and comprehensive risk measure for extreme scenarios.
Advantages and Limitations of CVaR
Conditional Value at Risk (CVaR) offers a more comprehensive risk assessment than Value at Risk (VaR) by measuring the expected loss given that losses exceed the VaR threshold, capturing tail risk in extreme market conditions. CVaR addresses VaR's limitation of ignoring loss magnitudes beyond the cutoff point, making it especially valuable for portfolios with fat-tailed or skewed return distributions. However, CVaR's computational complexity and sensitivity to distributional assumptions can pose challenges in practical risk management applications.
Choosing Between VaR and CVaR: Which is Better?
Value at Risk (VaR) measures the maximum potential loss over a specified period at a given confidence level, while Conditional Value at Risk (CVaR) estimates the expected loss exceeding the VaR threshold, providing a more comprehensive risk assessment. CVaR is often preferred by risk managers seeking to capture tail risk and account for extreme losses beyond VaR, especially in volatile or non-normal return distributions. Choosing between VaR and CVaR depends on the risk tolerance and regulatory requirements, with CVaR offering better sensitivity to extreme market conditions and a more coherent risk measure for portfolio optimization.
Conclusion: Aligning Risk Measures with Portfolio Goals
Value at Risk (VaR) provides a threshold loss level under normal market conditions, while Conditional Value at Risk (CVaR) evaluates expected losses beyond the VaR, capturing tail risk more comprehensively. Aligning these risk measures with portfolio goals depends on the investor's risk tolerance and the need for downside protection; portfolios seeking to minimize extreme losses benefit more from CVaR analysis. Incorporating CVaR into risk management offers a nuanced understanding of potential losses, enhancing strategic decisions for robust portfolio optimization.
Value at Risk Infographic
 libterm.com
libterm.com