The Lorenz curve visually represents income or wealth distribution within a population, highlighting inequality levels by plotting cumulative percentages of total income against cumulative population percentages. Understanding this curve helps you analyze economic disparities and assess social equity more effectively. Explore the rest of the article to learn how the Lorenz curve is constructed and interpreted in detail.
Table of Comparison
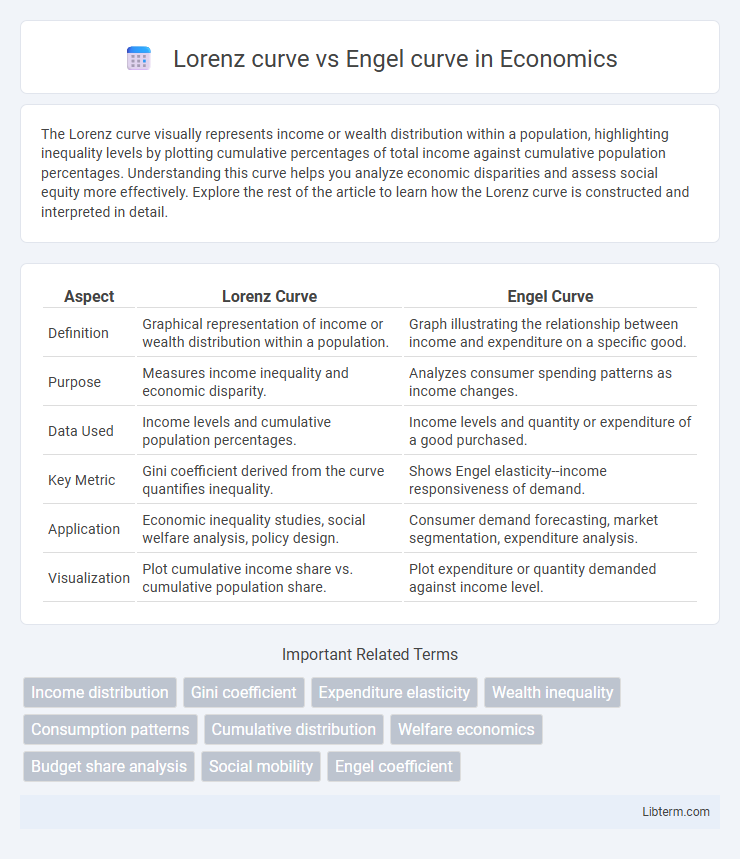
| Aspect | Lorenz Curve | Engel Curve |
|---|---|---|
| Definition | Graphical representation of income or wealth distribution within a population. | Graph illustrating the relationship between income and expenditure on a specific good. |
| Purpose | Measures income inequality and economic disparity. | Analyzes consumer spending patterns as income changes. |
| Data Used | Income levels and cumulative population percentages. | Income levels and quantity or expenditure of a good purchased. |
| Key Metric | Gini coefficient derived from the curve quantifies inequality. | Shows Engel elasticity--income responsiveness of demand. |
| Application | Economic inequality studies, social welfare analysis, policy design. | Consumer demand forecasting, market segmentation, expenditure analysis. |
| Visualization | Plot cumulative income share vs. cumulative population share. | Plot expenditure or quantity demanded against income level. |
Introduction to Lorenz Curve and Engel Curve
The Lorenz curve graphically represents income or wealth distribution within a population, illustrating inequality by plotting cumulative population percentages against cumulative income shares. The Engel curve depicts the relationship between household income and expenditure on a particular good, showing how consumption changes as income varies. Both curves are fundamental in economic analysis, with the Lorenz curve emphasizing income inequality and the Engel curve highlighting consumer behavior patterns.
Defining the Lorenz Curve
The Lorenz curve represents the distribution of income or wealth within a population, plotting the cumulative percentage of total income earned against the cumulative percentage of recipients, beginning with the poorest individual or household. It serves as a fundamental tool in economics to measure inequality and visualize disparities in income distribution. Unlike the Engel curve, which relates income to expenditure on a specific good, the Lorenz curve offers a comprehensive overview of overall economic inequality.
Understanding the Engel Curve
The Engel curve illustrates the relationship between household income and expenditure on a particular good, showing how consumption patterns change as income varies. Unlike the Lorenz curve, which measures income inequality across a population, the Engel curve is used to analyze consumer behavior and demand elasticity. Understanding the Engel curve helps economists determine whether a good is a necessity or a luxury based on how spending adjusts with income changes.
Key Differences between Lorenz and Engel Curves
The Lorenz curve graphically represents income or wealth distribution within a population, highlighting inequality by plotting cumulative income against the cumulative population percentage. In contrast, the Engel curve illustrates the relationship between household income and expenditure on a specific good, showing how consumption patterns change with income variations. Key differences include the Lorenz curve's focus on overall income distribution and inequality measurement, whereas the Engel curve emphasizes consumer behavior and demand elasticity for particular goods based on income changes.
Mathematical Representation of Lorenz and Engel Curves
The Lorenz curve is mathematically represented as L(p) = (1/m) 0^p F^(-1)(t) dt, where L(p) denotes the cumulative share of income earned by the bottom p proportion of the population, m is the mean income, and F^(-1)(t) is the income quantile function. The Engel curve is expressed as E(x) = E_i(x_i) = f(w_i, p_i), showing the relationship between household expenditure on a good (x_i) and household income or total expenditure (w_i), often modeled as a function dependent on prices (p_i) and income. Both curves provide valuable insights: the Lorenz curve measures income inequality via cumulative distributions, while the Engel curve characterizes consumption patterns as income varies.
Applications in Economics and Income Distribution
The Lorenz curve is a key tool in economics for illustrating income distribution and measuring inequality within a population, often used to calculate the Gini coefficient. The Engel curve, by contrast, analyzes consumer spending patterns by showing the relationship between household income and expenditure on a particular good, helping economists understand demand elasticity and consumer behavior. Both curves provide valuable insights into economic welfare: the Lorenz curve informs policy design targeting income redistribution, while the Engel curve guides market segmentation and poverty assessment.
Graphical Interpretation: Lorenz vs Engel Curves
The Lorenz curve graphically represents income or wealth distribution, displaying cumulative population percentages on the x-axis against cumulative income shares on the y-axis, thus highlighting inequality through the curve's deviation from the line of equality. In contrast, the Engel curve illustrates the relationship between income levels and expenditure on a particular good, plotting income on the x-axis and quantity demanded or spending on the y-axis, showing how consumption patterns change with income. While the Lorenz curve measures distribution inequality, the Engel curve focuses on consumer behavior across income variations, offering distinct insights through their respective graphical interpretations.
Limitations and Assumptions of Each Curve
The Lorenz curve assumes a continuous distribution of income within a population and may oversimplify income inequality by not capturing multidimensional aspects such as wealth or access to services, limiting its use in comprehensive economic analysis. The Engel curve presupposes stable consumer preferences and income-consumption relationships, yet it struggles to account for variations in price changes, cultural factors, or non-monetary benefits impacting consumption patterns. Both curves face limitations in representing dynamic economic behaviors over time, as the Lorenz curve is static and the Engel curve often neglects shifts in consumer priorities or external economic shocks.
Real-World Examples and Case Studies
The Lorenz curve provides a graphical representation of income inequality within a population, often utilized in studies such as the 2019 World Bank report on global wealth distribution, which showed stark disparities between countries like South Africa and Sweden. The Engel curve illustrates the relationship between household income and expenditure on a particular good, evidenced by a 2022 Chinese household dataset revealing increased spending on luxury food items as incomes rise. Case studies comparing Lorenz and Engel curves highlight how income inequality affects consumption patterns, as seen in Brazil's urban areas where higher income inequality correlates with slower growth in essential goods consumption.
Conclusion: Choosing the Right Curve for Economic Analysis
The Lorenz curve effectively measures income inequality by illustrating the distribution of wealth across a population, making it ideal for analyzing economic disparity and social welfare. The Engel curve, on the other hand, demonstrates the relationship between income levels and consumer expenditure patterns, providing insights into demand elasticity and household consumption behavior. Selecting the appropriate curve depends on whether the focus is on income distribution assessment or the analysis of consumption responses to income changes in economic research.
Lorenz curve Infographic
 libterm.com
libterm.com