Tower property refers to land or structures designated for the installation of communication towers, such as cellular, radio, or broadcasting towers. These properties often require specific zoning, permits, and lease agreements to support infrastructure that enables wireless communication services. Explore the rest of the article to understand how tower property impacts your connectivity and investment opportunities.
Table of Comparison
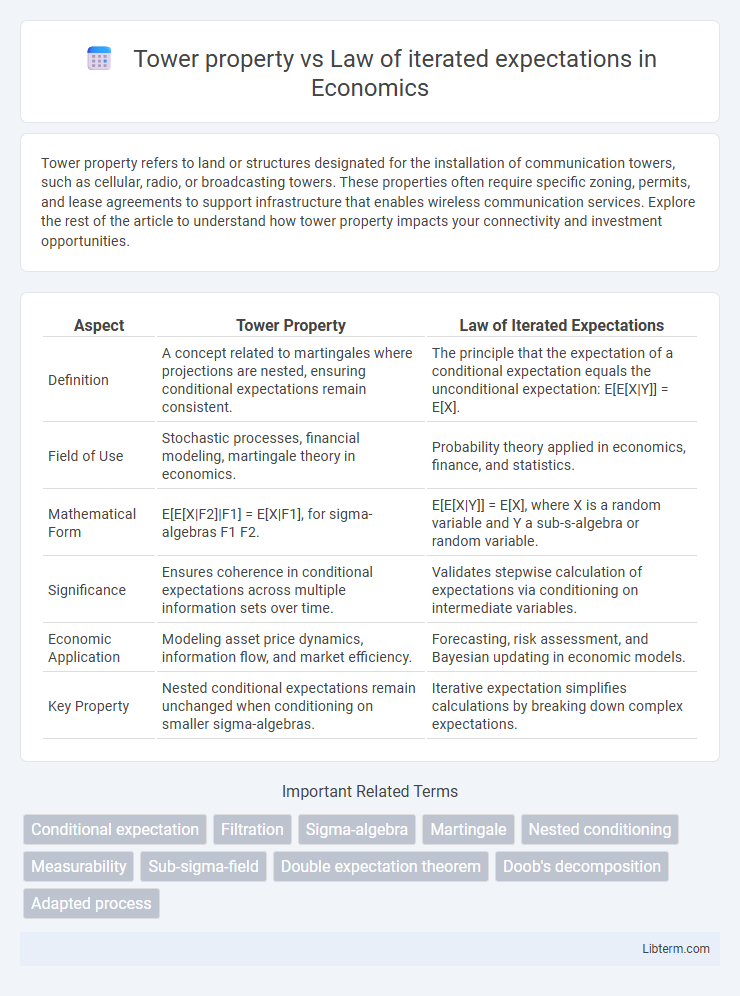
| Aspect | Tower Property | Law of Iterated Expectations |
|---|---|---|
| Definition | A concept related to martingales where projections are nested, ensuring conditional expectations remain consistent. | The principle that the expectation of a conditional expectation equals the unconditional expectation: E[E[X|Y]] = E[X]. |
| Field of Use | Stochastic processes, financial modeling, martingale theory in economics. | Probability theory applied in economics, finance, and statistics. |
| Mathematical Form | E[E[X|F2]|F1] = E[X|F1], for sigma-algebras F1 F2. | E[E[X|Y]] = E[X], where X is a random variable and Y a sub-s-algebra or random variable. |
| Significance | Ensures coherence in conditional expectations across multiple information sets over time. | Validates stepwise calculation of expectations via conditioning on intermediate variables. |
| Economic Application | Modeling asset price dynamics, information flow, and market efficiency. | Forecasting, risk assessment, and Bayesian updating in economic models. |
| Key Property | Nested conditional expectations remain unchanged when conditioning on smaller sigma-algebras. | Iterative expectation simplifies calculations by breaking down complex expectations. |
Introduction to Tower Property and Law of Iterated Expectations
The Tower Property, also known as the Law of Iterated Expectations, states that the expected value of a conditional expectation is equal to the unconditional expectation, formally expressed as E[E[X|Y]] = E[X]. This principle plays a crucial role in probability theory and statistics, providing a systematic way to simplify the computation of complex expectations by breaking them down into nested conditional expectations. Understanding this property is essential for applications in areas such as stochastic processes, econometrics, and financial modeling.
Defining the Tower Property in Probability Theory
The Tower Property in probability theory states that the conditional expectation of a random variable, given a coarser sigma-algebra, is equal to the conditional expectation of the conditional expectation given a finer sigma-algebra. It ensures consistency in nested conditional expectations, expressed as E[E[X | Y, Z] | Y] = E[X | Y]. This property underlies the Law of Iterated Expectations, which simplifies complex probabilistic computations by breaking down expectations stepwise.
Understanding the Law of Iterated Expectations
The Law of Iterated Expectations states that the expectation of a conditional expectation equals the unconditional expectation, mathematically expressed as E[E[X|Y]] = E[X]. This property ensures consistency in probabilistic modeling by allowing nested conditional expectations to be simplified without loss of information. Understanding this law is crucial in statistics, econometrics, and machine learning for unbiased estimation and sequential decision-making processes.
Mathematical Formulation of the Tower Property
The Tower Property, mathematically expressed as E[E[X|F2]|F1] = E[X|F1] for s-algebras F1 F2, underlies the Law of Iterated Expectations by ensuring consistent conditional expected values. This property formalizes how nested conditional expectations reduce stepwise, preserving the expectation relative to the smaller sigma-algebra. It is foundational in stochastic processes and martingale theory for simplifying complex conditional expectations.
Applications of the Law of Iterated Expectations
The Law of Iterated Expectations is extensively applied in econometrics and finance to simplify complex conditional expectation calculations by breaking them down into nested expectations. It plays a critical role in time series analysis, allowing for sequential updating of forecasts and risk assessments based on new information. This law underpins models like the Kalman filter and stochastic processes, where iterated conditioning facilitates estimation and inference in dynamic systems.
Relationship Between Tower Property and Conditional Expectation
The Tower Property, also known as the law of total expectation, establishes that the conditional expectation of a random variable given a coarser sigma-algebra equals the iterated conditional expectation conditioned on a finer sigma-algebra. This property ensures coherence between nested conditional expectations and underpins the consistency of conditional expectations in probability theory. Consequently, the Tower Property formalizes the relationship where E[E[X|G]|H] = E[X|H] for sigma-algebras H G, highlighting the fundamental structure of conditional expectation operators.
Key Differences: Tower Property vs. Law of Iterated Expectations
The Tower Property provides a general framework for nested conditional expectations, stating that taking an expectation multiple times with respect to increasing sigma-algebras simplifies to a single conditional expectation. The Law of Iterated Expectations specifically asserts that the unconditional expectation of a random variable equals the expectation of its conditional expectation given another variable. Key differences lie in scope and usage: the Tower Property applies broadly to nested filtrations in probability theory, while the Law of Iterated Expectations focuses on iterated conditioning over random variables.
Examples Illustrating Both Concepts
The Tower Property, a fundamental result in conditional expectation, states that E[E[X|Y]|Z] = E[X|Z] when Z is a sigma-algebra contained in Y, which can be illustrated by considering nested filtrations in a stochastic process like Brownian motion. The Law of Iterated Expectations (LIE) asserts that E[X] = E[E[X|Y]] and is often demonstrated with examples such as rolling a die and then flipping a coin conditional on the die outcome, showing how expected values simplify through conditioning. Both concepts are crucial in probability theory and econometrics for breaking down complex conditional expectations into simpler, nested components, enabling clearer insights into information structures and decision-making under uncertainty.
Importance in Statistics and Stochastic Processes
Tower property, also known as the law of total expectation, is fundamental in statistics and stochastic processes for simplifying complex conditional expectations by breaking them down into nested layers. It ensures consistency in expectation calculations across multiple sigma-algebras, enabling efficient analysis of dependent random variables and filtration in martingale theory. This property is crucial for deriving key results in time series analysis, Bayesian inference, and sequential decision-making under uncertainty.
Conclusion: When to Use Each Principle
The Tower Property is ideal for simplifying conditional expectations by iteratively conditioning on nested sigma-algebras, streamlining computations in stochastic processes and martingales. The Law of Iterated Expectations applies broadly to any integrable random variable, ensuring the consistency of expected values when conditioning on coarser sigma-algebras. Use the Tower Property when dealing with multistage conditional expectations within filtrations, while the Law of Iterated Expectations serves as a fundamental principle for expectation equivalences in probability theory.
Tower property Infographic
 libterm.com
libterm.com