Walrasian equilibrium represents a state in an economy where supply equals demand across all markets simultaneously, ensuring efficient resource allocation. This concept is foundational in general equilibrium theory, providing insights into market stability and price formation. Explore the full article to understand how Walrasian equilibrium shapes economic analysis and your interpretation of market dynamics.
Table of Comparison
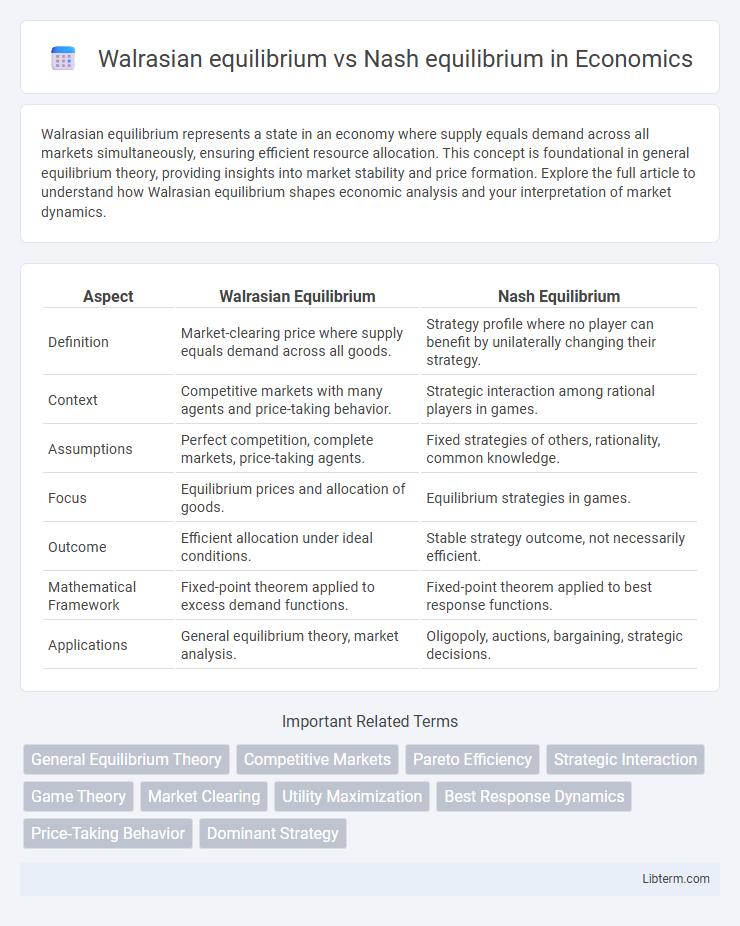
| Aspect | Walrasian Equilibrium | Nash Equilibrium |
|---|---|---|
| Definition | Market-clearing price where supply equals demand across all goods. | Strategy profile where no player can benefit by unilaterally changing their strategy. |
| Context | Competitive markets with many agents and price-taking behavior. | Strategic interaction among rational players in games. |
| Assumptions | Perfect competition, complete markets, price-taking agents. | Fixed strategies of others, rationality, common knowledge. |
| Focus | Equilibrium prices and allocation of goods. | Equilibrium strategies in games. |
| Outcome | Efficient allocation under ideal conditions. | Stable strategy outcome, not necessarily efficient. |
| Mathematical Framework | Fixed-point theorem applied to excess demand functions. | Fixed-point theorem applied to best response functions. |
| Applications | General equilibrium theory, market analysis. | Oligopoly, auctions, bargaining, strategic decisions. |
Introduction to Walrasian and Nash Equilibrium
Walrasian equilibrium, also known as competitive equilibrium, occurs when supply equals demand in all markets resulting from price adjustments by a hypothetical auctioneer, ensuring market clearing without excess supply or demand. Nash equilibrium, fundamental in game theory, describes a situation where no player can improve their payoff by unilaterally changing their strategy, given the strategies of others. Both concepts model strategic interaction and market outcomes, with Walrasian equilibrium emphasizing price-taking behavior in perfectly competitive markets and Nash equilibrium capturing the strategic decision-making of interdependent agents.
Defining Walrasian Equilibrium
Walrasian equilibrium, also known as competitive equilibrium, is defined by a state where supply equals demand across all markets, and prices adjust accordingly to clear markets with no excess supply or demand. This equilibrium assumes perfectly competitive markets, price-taking behavior by agents, and complete information, ensuring that no participant can improve their utility by unilaterally changing their strategy. Unlike Nash equilibrium, which focuses on strategic interactions among players with individual payoffs, Walrasian equilibrium centers on price mechanisms coordinating decentralized decisions in an economy.
Understanding Nash Equilibrium
Nash equilibrium occurs in strategic games where each player's strategy is optimal given the strategies of others, resulting in no incentive for unilateral deviation. Unlike Walrasian equilibrium, which models market-wide supply and demand balance with price adjustments, Nash equilibrium analyzes individual decision-making in competitive settings with interdependent choices. Understanding Nash equilibrium provides insight into predicting stable outcomes in oligopolies, auctions, and negotiations where players anticipate rivals' behavior.
Key Differences Between Walrasian and Nash Equilibrium
Walrasian equilibrium involves a competitive market setting where prices adjust to equalize supply and demand, leading to an efficient allocation of resources under perfect competition assumptions. Nash equilibrium occurs in strategic games where each player optimizes their strategy given others' strategies, without price adjustments driving outcomes. Key differences include the role of prices in Walrasian equilibrium versus strategic decision-making in Nash equilibrium, and the assumption of market-clearing versus individual rationality in game theory contexts.
Mathematical Formulations and Assumptions
Walrasian equilibrium is defined by a system of equations where supply equals demand in every market, based on assumptions of perfectly competitive markets, price-taking agents, and market-clearing prices; the mathematical formulation relies on solving \(\sum_i x_i(p) = \sum_i e_i\) for price vector \(p\). Nash equilibrium is characterized by a set of strategies where no player can improve their payoff unilaterally, formulated through best-response functions and fixed points in strategy space, expressed as \(s_i^* = \arg\max_{s_i} u_i(s_i, s_{-i}^*)\) for each player \(i\). Walrasian equilibrium assumes homogeneous goods and complete markets, while Nash equilibrium allows for strategic interdependence and potentially asymmetric information among players.
Applications in Economic Theory
Walrasian equilibrium models idealized markets where supply equals demand through price adjustments, extensively applied in general equilibrium analysis to predict market outcomes and resource allocations. Nash equilibrium, grounded in game theory, analyzes strategic interactions among agents, widely used in oligopoly market structures, auction designs, and bargaining problems. Both concepts underpin modern economic theory by providing frameworks for understanding competitive markets and strategic behavior in economic environments.
Strengths and Limitations of Walrasian Equilibrium
Walrasian equilibrium excels in modeling perfectly competitive markets with complete information, ensuring price-taking behavior leads to market-clearing prices where supply equals demand. Its strength lies in providing a comprehensive framework for analyzing resource allocation efficiency under idealized conditions, but it assumes the existence of a price vector that balances markets, which may not hold in real-world scenarios with imperfect competition or incomplete markets. Limitations include the inability to capture strategic interactions among agents and the reliance on assumptions of perfect competition and perfect information, unlike Nash equilibrium that explicitly incorporates strategic decision-making in non-cooperative games.
Strengths and Limitations of Nash Equilibrium
Nash equilibrium excels in modeling strategic interactions where each player's optimal decision depends on others' choices, providing insights into competitive behaviors in economics, political science, and evolutionary biology. Its strengths lie in predicting stable outcomes without requiring cooperation or enforced agreements, applicable in non-cooperative games and oligopolistic markets. Limitations include potential multiple or no equilibria, lack of efficiency guarantees, and assumptions of perfect rationality and common knowledge, which may reduce real-world applicability.
Real-World Examples: Walrasian vs Nash Equilibrium
Walrasian equilibrium is commonly observed in perfectly competitive markets like agricultural commodity trading where prices adjust to clear supply and demand, ensuring efficient resource allocation. Nash equilibrium appears in strategic settings such as oligopolistic industries like telecommunications, where firms set prices or quantities based on competitors' expected actions to maximize their payoffs. Real-world applications demonstrate that Walrasian models suit markets with price-taking agents, while Nash equilibria better capture scenarios involving strategic interaction and market power.
Conclusion: Choosing the Right Equilibrium Concept
Selecting the appropriate equilibrium concept depends on the economic context and strategic interactions involved. Walrasian equilibrium suits competitive markets with price-taking agents and complete markets, emphasizing market-clearing prices and resource allocation efficiency. Nash equilibrium better captures strategic behavior in games where agents anticipate others' decisions, essential for analyzing oligopolies and strategic market settings.
Walrasian equilibrium Infographic
 libterm.com
libterm.com