The stochastic discount factor (SDF) plays a crucial role in asset pricing by linking future uncertain payoffs to current prices through a probabilistic framework. It captures investors' risk preferences and time value of money, enabling accurate valuation of financial securities under uncertainty. Discover how understanding the stochastic discount factor can enhance your investment decisions by exploring the rest of this article.
Table of Comparison
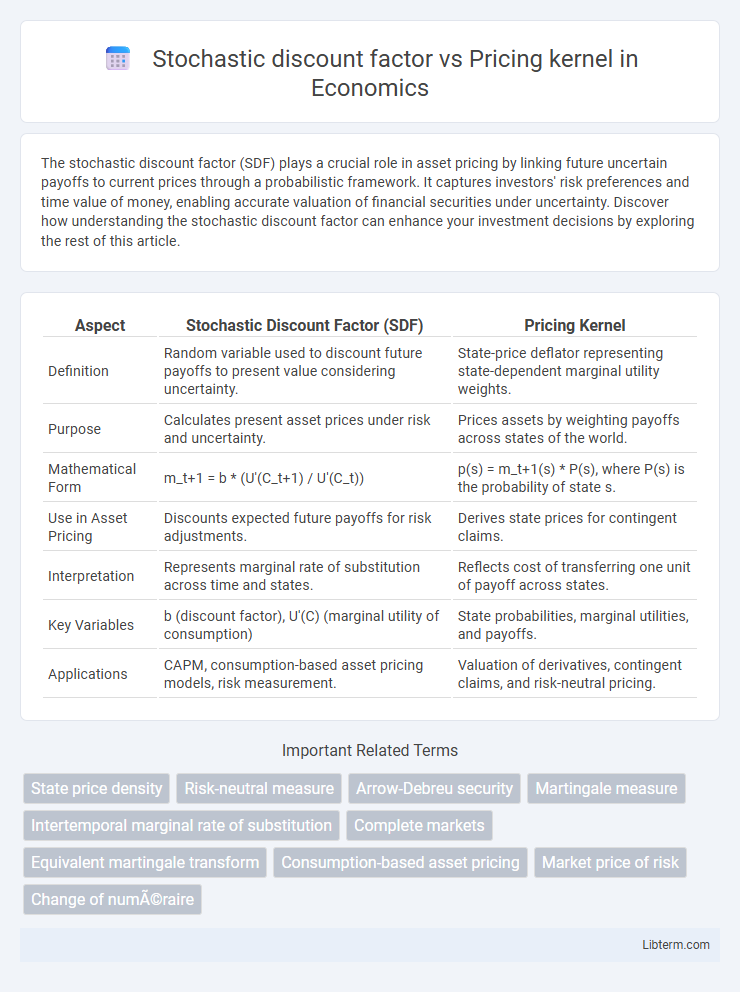
| Aspect | Stochastic Discount Factor (SDF) | Pricing Kernel |
|---|---|---|
| Definition | Random variable used to discount future payoffs to present value considering uncertainty. | State-price deflator representing state-dependent marginal utility weights. |
| Purpose | Calculates present asset prices under risk and uncertainty. | Prices assets by weighting payoffs across states of the world. |
| Mathematical Form | m_t+1 = b * (U'(C_t+1) / U'(C_t)) | p(s) = m_t+1(s) * P(s), where P(s) is the probability of state s. |
| Use in Asset Pricing | Discounts expected future payoffs for risk adjustments. | Derives state prices for contingent claims. |
| Interpretation | Represents marginal rate of substitution across time and states. | Reflects cost of transferring one unit of payoff across states. |
| Key Variables | b (discount factor), U'(C) (marginal utility of consumption) | State probabilities, marginal utilities, and payoffs. |
| Applications | CAPM, consumption-based asset pricing models, risk measurement. | Valuation of derivatives, contingent claims, and risk-neutral pricing. |
Introduction to Stochastic Discount Factor and Pricing Kernel
The stochastic discount factor (SDF) and pricing kernel are fundamental concepts in asset pricing, representing the same mathematical tool used to discount future payoffs to present value while accounting for risk. The SDF is a random variable that adjusts payoffs under uncertainty by incorporating investors' marginal utility of consumption or wealth, effectively capturing risk preferences and time value of money. The pricing kernel, often used interchangeably with the SDF, serves as a state-price deflator that links asset prices to their future cash flows within a unified framework in financial economics.
Core Concepts: What is a Stochastic Discount Factor?
The Stochastic Discount Factor (SDF) is a fundamental concept in financial economics used to price uncertain future cash flows by adjusting them for risk and time value of money. It represents the state-price density or the marginal rate of substitution in consumption, linking asset payoffs to their present values through expectations under a risk-neutral measure. The pricing kernel is essentially the same as the SDF, serving as a mathematical function that discounts stochastic payoffs to present values, reflecting market risk preferences and equilibrium conditions.
Pricing Kernel: Definition and Mathematical Formulation
The pricing kernel, also known as the stochastic discount factor (SDF), is a fundamental concept in financial economics used to price risky assets by discounting their payoffs to present values. Mathematically, the pricing kernel \(m_t\) is defined as the ratio of the marginal utility of consumption across states, expressed as \(m_t = \beta \frac{u'(C_{t+1})}{u'(C_t)}\), where \(\beta\) is the subjective discount factor and \(u'\) represents the marginal utility function. This kernel facilitates the valuation of any asset's payoff \(X_{t+1}\) through the relation \(P_t = \mathbb{E}_t[m_{t+1} X_{t+1}]\), linking consumption-based asset pricing to state prices and risk preferences.
The Relationship between SDF and Pricing Kernel
The Stochastic Discount Factor (SDF) and the Pricing Kernel are fundamentally equivalent concepts used to price risky assets by discounting future payoffs to their present value through a state-dependent multiplier. The SDF represents the intertemporal marginal rate of substitution in consumption, while the Pricing Kernel is the state price density that adjusts payoffs for risk preferences and probability distortions. The relationship between the SDF and Pricing Kernel is that the SDF can be interpreted as the Pricing Kernel normalized by the probability measure, connecting asset prices directly to investors' risk preferences and market states.
Role in Asset Pricing Theory
The stochastic discount factor (SDF) serves as a fundamental concept in asset pricing theory by representing the state-price density that discounts future payoffs to present values under uncertainty. The pricing kernel, often used interchangeably with the SDF, embodies investors' marginal utility of wealth and captures risk preferences, enabling the equilibrium pricing of risky assets. Both concepts are central to linking market prices with consumption-based utility models and expected returns, providing a unified framework for understanding asset valuation under risk.
Mathematical Derivation and Interpretation
The stochastic discount factor (SDF) and pricing kernel are mathematically equivalent concepts used in asset pricing to discount future payoffs to their present value. The SDF \(m_t\) satisfies the fundamental pricing equation \(P_t = \mathbb{E}_t [ m_{t+1} X_{t+1} ]\), where \(X_{t+1}\) is a future payoff and \(\mathbb{E}_t\) denotes the conditional expectation. Interpretively, the pricing kernel represents state prices or marginal utilities of consumption, linking investor preferences with risk-neutral probabilities in the valuation of contingent claims.
Applications in Financial Modeling
Stochastic discount factors and pricing kernels are fundamental tools in asset pricing and risk management within financial modeling. The stochastic discount factor serves as a state-price density reflecting the present value of future payoffs under uncertainty, essential for valuing derivatives and optimizing portfolios. Pricing kernels, representing the marginal utility of consumption, enable the measurement of risk preferences and market equilibrium, facilitating the calibration of models like the Capital Asset Pricing Model (CAPM) and consumption-based asset pricing frameworks.
Comparative Analysis: SDF vs Pricing Kernel
The stochastic discount factor (SDF) and pricing kernel both serve as central tools in asset pricing, linking future payoffs to present values by incorporating risk preferences and state probabilities. While the SDF is a multiplicative factor adjusting for risk and time in expected payoffs, the pricing kernel specifically represents the marginal utility of consumption across states, often providing an economically grounded interpretation of discounting. Comparative analysis highlights that the SDF is a more general mathematical construct applicable in diverse models, whereas the pricing kernel emphasizes the utility-based perspective, enabling clearer insights into investor behavior and equilibrium asset prices.
Common Misconceptions
The stochastic discount factor (SDF) and pricing kernel are often mistakenly treated as distinct concepts, but they are mathematically equivalent tools used to price risky assets by discounting payoffs to present value. A common misconception is that the SDF is only a theoretical construct, whereas the pricing kernel is interpreted as a state-price density; in reality, both represent the same underlying state-dependent discounting mechanism. Confusion also arises in empirical asset pricing where the terminology varies by discipline, yet recognizing their equivalence clarifies model calibration and risk-neutral valuation.
Conclusion: Implications for Financial Research
The stochastic discount factor and pricing kernel fundamentally represent equivalent tools for asset pricing, with the former emphasizing discounting mechanisms and the latter highlighting state-price densities. Understanding their duality enhances model consistency and accuracy in estimating risk premia and asset returns. This equivalence guides financial research to integrate stochastic discount factor methods with pricing kernel frameworks, fostering robust empirical asset pricing and improving risk management strategies.
Stochastic discount factor Infographic
 libterm.com
libterm.com