The Laffer curve illustrates the relationship between tax rates and tax revenue, showing that increasing tax rates beyond a certain point can actually reduce total revenue. Understanding this economic concept helps policymakers design tax systems that optimize revenue without discouraging work or investment. Discover how the Laffer curve can impact your financial decisions by reading the rest of this article.
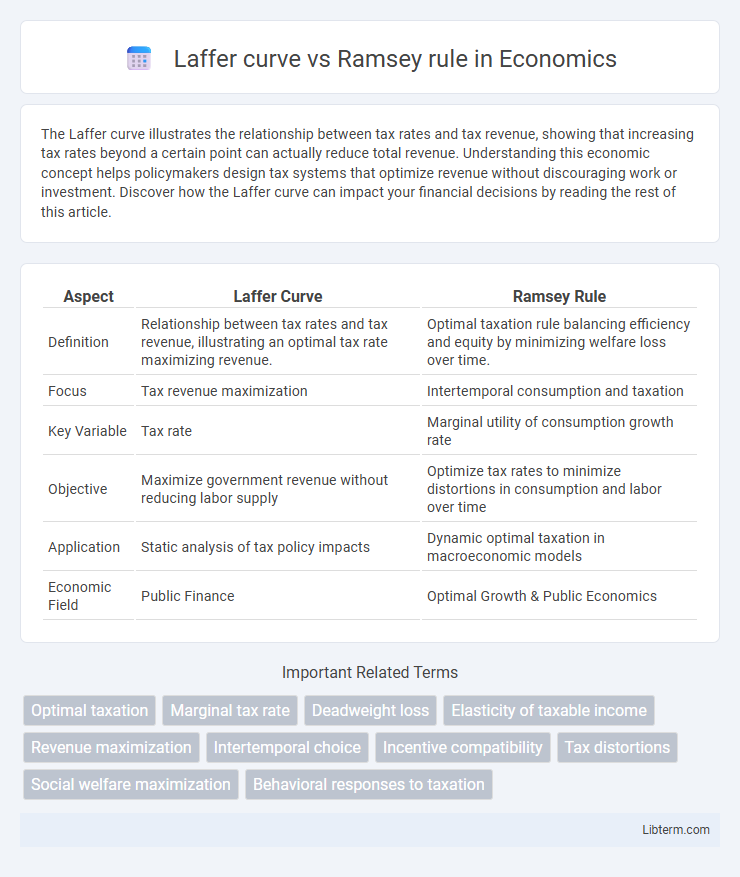
Table of Comparison
| Aspect | Laffer Curve | Ramsey Rule |
|---|---|---|
| Definition | Relationship between tax rates and tax revenue, illustrating an optimal tax rate maximizing revenue. | Optimal taxation rule balancing efficiency and equity by minimizing welfare loss over time. |
| Focus | Tax revenue maximization | Intertemporal consumption and taxation |
| Key Variable | Tax rate | Marginal utility of consumption growth rate |
| Objective | Maximize government revenue without reducing labor supply | Optimize tax rates to minimize distortions in consumption and labor over time |
| Application | Static analysis of tax policy impacts | Dynamic optimal taxation in macroeconomic models |
| Economic Field | Public Finance | Optimal Growth & Public Economics |
Introduction to the Laffer Curve and Ramsey Rule
The Laffer Curve illustrates the relationship between tax rates and tax revenue, demonstrating that beyond a certain point, higher tax rates lead to decreased revenue due to diminished economic incentives. The Ramsey Rule guides optimal taxation by minimizing distortions in consumption choices, prescribing lower tax rates on goods with inelastic demand to improve overall welfare. Both concepts analyze tax efficiency but approach it from distinct perspectives: revenue maximization versus welfare optimization.
Historical Background and Theoretical Foundations
The Laffer Curve, developed by economist Arthur Laffer in the 1970s, illustrates the relationship between tax rates and tax revenue, emphasizing the point at which higher tax rates decrease total revenue due to diminished incentives to work and invest. In contrast, the Ramsey Rule, formulated by Frank P. Ramsey in 1927, provides a framework for optimal taxation that minimizes economic distortions by setting tax rates inversely proportional to the price elasticity of demand, ensuring efficient resource allocation. Both concepts emerged from efforts to balance government revenue needs with economic efficiency, but they prioritize different aspects: the Laffer Curve focuses on behavioral responses to taxation, while the Ramsey Rule emphasizes welfare maximization through distortion minimization.
Key Assumptions of the Laffer Curve
The Laffer Curve assumes a nonlinear relationship between tax rates and tax revenue, where increasing tax rates beyond a certain point leads to decreased revenue due to diminished economic activity and incentives. It presupposes that individuals respond to taxation by altering labor supply, investment, or work effort, causing taxable income to fluctuate. This model relies on dynamic behavioral responses rather than static tax base assumptions, contrasting with the Ramsey rule's focus on minimizing welfare loss through efficient taxation.
Core Principles of the Ramsey Rule
The Ramsey Rule centers on minimizing the distortionary costs of taxation by equalizing the marginal deadweight loss across all taxed goods, ensuring efficient allocation of resources. It advocates for taxing goods inversely proportional to their price elasticity of demand, so goods with inelastic demand bear higher taxes, reducing overall economic inefficiency. Unlike the Laffer Curve, which emphasizes revenue maximization through tax rate adjustments, the Ramsey Rule focuses on balancing tax rates to minimize welfare loss in optimal tax policy design.
Comparative Analysis: Revenue Maximization vs. Welfare Optimization
The Laffer curve illustrates the relationship between tax rates and tax revenue, emphasizing revenue maximization by identifying an optimal tax rate that maximizes government income without discouraging work or investment. In contrast, the Ramsey rule prioritizes welfare optimization by suggesting differentiated tax rates to minimize the excess burden of taxation on consumption goods, aiming to maintain economic efficiency and social welfare. While the Laffer curve focuses on maximizing revenue capacity, the Ramsey rule balances tax distortions to enhance overall welfare, reflecting distinct fiscal policy objectives.
Policy Implications for Tax Design
The Laffer curve illustrates the trade-off between tax rates and tax revenue, emphasizing that excessively high tax rates can reduce incentives to work or invest and thereby shrink tax revenue. In contrast, the Ramsey rule advocates for minimizing economic distortions by setting tax rates inversely proportional to the elasticity of demand for goods, promoting efficiency in revenue generation. Policymakers must balance these insights by avoiding overly aggressive taxation that stifles economic activity while strategically targeting taxes on inelastic goods to optimize revenue without substantial welfare loss.
Empirical Evidence and Real-World Applications
Empirical evidence for the Laffer Curve highlights the relationship between tax rates and revenue, showing diminishing returns beyond certain tax thresholds, as seen in U.S. and European tax reforms. The Ramsey Rule focuses on optimal taxation to minimize welfare loss by taxing inelastic goods more heavily, supported by studies on consumption patterns and labor supply elasticity. Real-world applications include supply-side tax cuts inspired by the Laffer Curve and differentiated commodity taxation based on the Ramsey Rule to improve economic efficiency.
Limitations and Criticisms of Each Approach
The Laffer curve faces criticism for its oversimplified depiction of the relationship between tax rates and revenue, often ignoring factors like behavioral responses and economic context that affect tax efficiency. The Ramsey rule, focused on minimizing welfare loss by setting taxes inversely proportional to price elasticities, is criticized for assuming perfect information and ignoring equity considerations in tax policy. Both approaches are limited by their theoretical assumptions and often fail to capture the complexity of real-world tax systems and economic behaviors.
Integrating Laffer and Ramsey Insights in Modern Tax Policy
Integrating Laffer curve and Ramsey rule insights in modern tax policy involves balancing revenue maximization with efficiency in taxation. The Laffer curve highlights the trade-off between tax rates and total revenue, emphasizing the risk of excessive taxation reducing incentives to work or invest. Ramsey rule guides optimal commodity taxation by minimizing excess burden, suggesting higher taxes on inelastic goods; combining these frameworks helps design tax systems that maximize revenue without distorting economic behavior significantly.
Conclusion: Navigating Trade-offs in Optimal Taxation
The Laffer curve illustrates the trade-off between tax rates and revenue generation, showing an optimal tax rate that maximizes revenue without discouraging labor supply. The Ramsey rule emphasizes minimizing economic distortions by setting tax rates inversely proportional to the elasticity of demand for goods. Balancing these models guides policymakers to design optimal taxation that maximizes revenue while minimizing economic inefficiencies and welfare losses.
Laffer curve Infographic
 libterm.com
libterm.com