Walrasian equilibrium represents a state in a competitive market where supply equals demand across all goods, resulting in market-clearing prices without excess surplus or shortage. This equilibrium concept is foundational in general equilibrium theory, helping economists understand how markets allocate resources efficiently. Explore the rest of the article to learn how Walrasian equilibrium shapes modern economic analysis and impacts your market interactions.
Table of Comparison
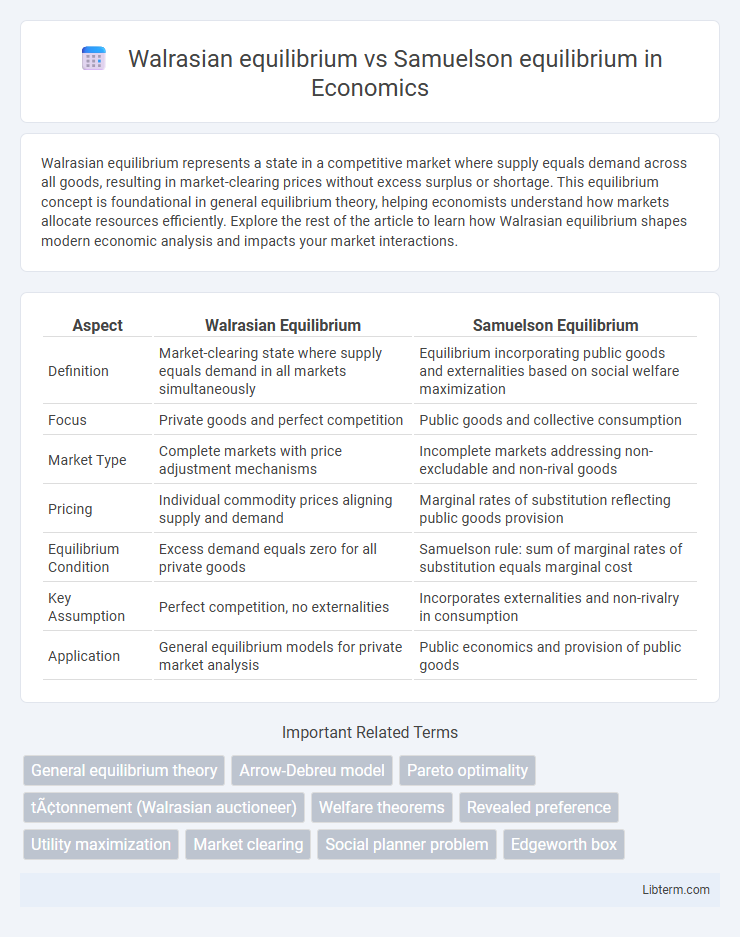
| Aspect | Walrasian Equilibrium | Samuelson Equilibrium |
|---|---|---|
| Definition | Market-clearing state where supply equals demand in all markets simultaneously | Equilibrium incorporating public goods and externalities based on social welfare maximization |
| Focus | Private goods and perfect competition | Public goods and collective consumption |
| Market Type | Complete markets with price adjustment mechanisms | Incomplete markets addressing non-excludable and non-rival goods |
| Pricing | Individual commodity prices aligning supply and demand | Marginal rates of substitution reflecting public goods provision |
| Equilibrium Condition | Excess demand equals zero for all private goods | Samuelson rule: sum of marginal rates of substitution equals marginal cost |
| Key Assumption | Perfect competition, no externalities | Incorporates externalities and non-rivalry in consumption |
| Application | General equilibrium models for private market analysis | Public economics and provision of public goods |
Introduction to Walrasian Equilibrium
Walrasian equilibrium, central to general equilibrium theory, describes a state where supply and demand across all markets simultaneously balance through price adjustments, ensuring no excess demand or supply exists. It relies on the assumption of perfectly competitive markets and rational agents optimizing utility and profits, leading to market-clearing prices. This concept contrasts with Samuelson equilibrium, which incorporates dynamic adjustments and expectations in macroeconomic contexts, emphasizing continuous adjustment processes beyond static price settings.
Foundations of Samuelson Equilibrium
Samuelson equilibrium builds on the Walrasian framework by incorporating uncertain future states into consumer and producer optimization problems, grounding the model in expected utility theory. This foundational shift allows for state-contingent commodity markets, where prices reflect probabilistic assessments, enabling a more comprehensive representation of risk and information. Samuelson's approach extends the general equilibrium concept to dynamic settings, providing a rigorous basis for analyzing optimal allocation under uncertainty.
Core Assumptions: Walras vs. Samuelson
Walrasian equilibrium assumes perfect competition, complete markets, and price-taking behavior, emphasizing market-clearing prices where supply equals demand across all goods. Samuelson's equilibrium relaxes some of these assumptions by incorporating imperfect competition, strategic interactions, and dynamic adjustments, focusing on stability and the role of expectations in market outcomes. The core distinction lies in Walras's static, idealized framework versus Samuelson's realistic, dynamic approach considering behavioral factors and market imperfections.
Mathematical Formulations Compared
Walrasian equilibrium is defined by a system of equations where prices adjust so that aggregate supply equals aggregate demand across all markets, relying on fixed-point theorems to prove existence. Samuelson equilibrium extends this by incorporating intertemporal optimization with a focus on dynamic efficiency, using variational inequalities and differential equations to capture time-dependent preferences and capital accumulation. The key mathematical difference lies in Walras's static equilibrium condition p * (D(p) - S(p)) = 0 compared to Samuelson's dynamic framework expressed through Euler equations and Hamiltonian systems.
Market Clearing Mechanisms
Walrasian equilibrium relies on a tatonnement process where prices adjust continuously until supply equals demand in all markets, ensuring market clearing without actual trades occurring during the price adjustment phase. Samuelson equilibrium extends this concept by incorporating uncertainty and time, focusing on intertemporal market clearing via contingent commodity markets, where prices reflect future states and trades clear across time and states. The key distinction lies in Walrasian equilibrium's static market clearing at a single time point versus Samuelson equilibrium's dynamic clearing that accounts for expectations and risk-sharing over multiple periods.
Role of Utility and Welfare in Each Model
Walrasian equilibrium emphasizes the role of individual utility maximization, where markets clear through price adjustments ensuring that supply equals demand, leading to Pareto efficiency in resource allocation. Samuelson equilibrium expands on this by incorporating social welfare functions, integrating individual utilities into a collective criterion that reflects societal preferences and equity considerations. The focus in Walrasian models is on decentralized decision-making and utility optimization at the personal level, while Samuelson's framework prioritizes the welfare economics perspective, assessing overall social welfare and potential policy implications.
Dynamic Versus Static Analysis
Walrasian equilibrium represents a static analysis framework where market prices adjust instantaneously to equate supply and demand, assuming perfect information and no time dynamics. In contrast, Samuelson equilibrium incorporates dynamic analysis by modeling how prices and allocations evolve over time under uncertainty and intertemporal optimization. This dynamic approach captures the temporal dimension of economic adjustments, emphasizing continuous adaptation rather than fixed-point market clearing.
Efficiency and Pareto Optimality
Walrasian equilibrium, defined by the simultaneous clearing of all markets through price adjustments, inherently achieves Pareto efficiency where no agent can be made better off without making another worse off. Samuelson equilibrium extends this concept to public goods, ensuring efficiency by equating the sum of marginal rates of substitution to the marginal cost of provision, thus achieving a form of Pareto optimality in the presence of non-excludable and non-rivalrous goods. While Walrasian equilibrium focuses on private goods markets, Samuelson equilibrium addresses the efficient allocation in public goods economies, both frameworks central to understanding general equilibrium efficiency and optimal resource distribution.
Criticisms and Limitations
Walrasian equilibrium faces criticisms for its reliance on perfect competition and complete markets, assumptions that rarely hold in real economies, limiting its applicability to practical scenarios. Samuelson equilibrium, while extending to infinite-dimensional commodity spaces and intertemporal settings, is criticized for its abstraction and mathematical complexity, which may obscure economic intuition and hinder empirical verification. Both equilibria struggle with incorporating market imperfections, information asymmetries, and real-world frictions, constraining their relevance in addressing dynamic and incomplete market environments.
Implications for Modern Economic Theory
Walrasian equilibrium, based on general equilibrium theory, models perfectly competitive markets where supply equals demand, providing foundational insights into price formation and resource allocation efficiency. Samuelson equilibrium extends this framework by incorporating dynamic optimization and productivity growth, enhancing the analysis of long-term economic growth and intertemporal choices. Together, these equilibria shape modern economic theory by integrating static market clearing with dynamic behavioral responses, influencing policy design and macroeconomic modeling.
Walrasian equilibrium Infographic
 libterm.com
libterm.com