The Colburn analogy is a key concept in heat transfer that relates heat, mass, and momentum transfer processes, simplifying the analysis of convective heat transfer by using dimensionless numbers like the Nusselt, Reynolds, and Prandtl numbers. It allows engineers to predict heat transfer coefficients in fluid flows based on easily measured mass transfer or momentum transfer data, enhancing design efficiency. Dive into the rest of the article to uncover how the Colburn analogy can optimize your thermal system designs.
Table of Comparison
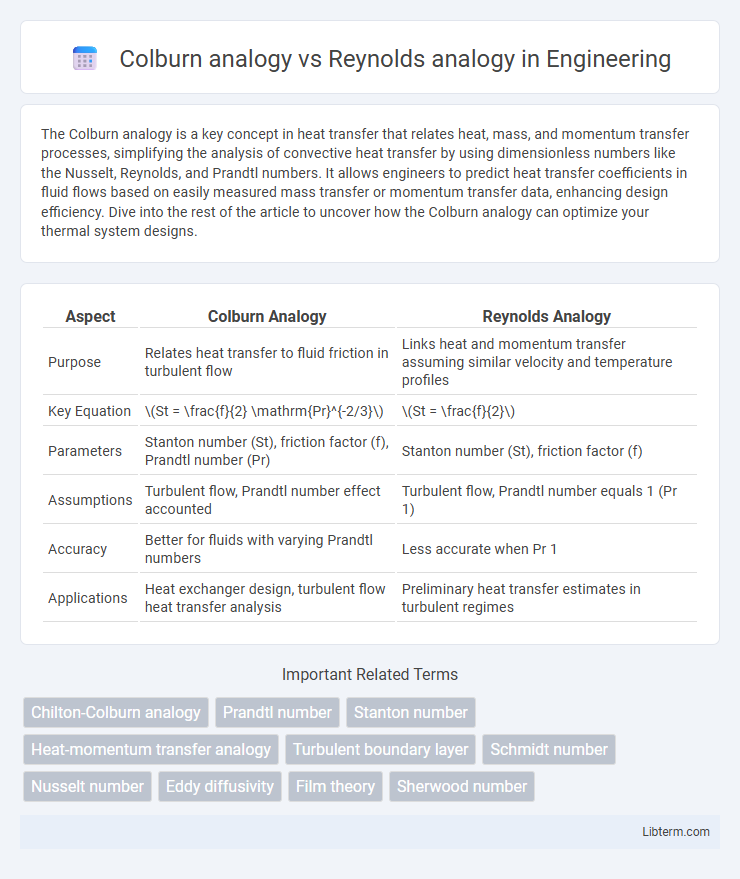
| Aspect | Colburn Analogy | Reynolds Analogy |
|---|---|---|
| Purpose | Relates heat transfer to fluid friction in turbulent flow | Links heat and momentum transfer assuming similar velocity and temperature profiles |
| Key Equation | \(St = \frac{f}{2} \mathrm{Pr}^{-2/3}\) | \(St = \frac{f}{2}\) |
| Parameters | Stanton number (St), friction factor (f), Prandtl number (Pr) | Stanton number (St), friction factor (f) |
| Assumptions | Turbulent flow, Prandtl number effect accounted | Turbulent flow, Prandtl number equals 1 (Pr 1) |
| Accuracy | Better for fluids with varying Prandtl numbers | Less accurate when Pr 1 |
| Applications | Heat exchanger design, turbulent flow heat transfer analysis | Preliminary heat transfer estimates in turbulent regimes |
Introduction to Heat and Momentum Transfer
The Colburn analogy relates heat transfer to momentum transfer by incorporating the Prandtl and Schmidt numbers, emphasizing the turbulent boundary layer's influence on convective heat and mass transfer. The Reynolds analogy simplifies this relationship by assuming equal turbulent diffusivities for momentum and heat, resulting in a direct correlation between the friction factor and heat transfer coefficient. Both analogies serve as foundational tools in understanding the interplay between heat and momentum transfer in fluid flow, crucial for designing efficient thermal systems.
Overview of Analogy Concepts in Fluid Mechanics
The Colburn analogy and Reynolds analogy are fundamental concepts in fluid mechanics that relate heat transfer to momentum transfer in turbulent flow. Colburn analogy introduces the j-factor, expressing the Stanton number in terms of the friction factor, enhancing prediction of convective heat transfer coefficients. Reynolds analogy simplifies the relationship by assuming equal turbulent diffusivities for momentum and heat, often providing a baseline for heat and mass transfer correlations in boundary layer analysis.
What is the Reynolds Analogy?
The Reynolds Analogy establishes a direct relationship between momentum and heat transfer in turbulent flow by equating the friction factor to the Stanton number, assuming similar transfer mechanisms for both phenomena. This analogy simplifies the prediction of convective heat transfer coefficients using known friction factors, primarily valid for fluids with Prandtl numbers close to one. Unlike the Colburn analogy, which introduces a corrective factor (j-factor) to account for differences in thermal and momentum diffusivities, the Reynolds analogy focuses on idealized conditions for matching velocity and temperature profiles.
What is the Colburn Analogy?
The Colburn analogy is a widely used correlation in heat transfer and fluid flow to relate the convective heat transfer coefficient to the friction factor and flow properties in turbulent flow conditions. It introduces the Colburn j-factor (j_H), which connects heat transfer coefficients to dimensionless parameters like the Reynolds number and Prandtl number, enhancing the prediction of heat transfer performance in pipes and ducts. Unlike the Reynolds analogy, which assumes equal turbulent heat and momentum transfer, the Colburn analogy incorporates the Prandtl number raised to the power of -2/3, providing greater accuracy for different fluid properties.
Mathematical Formulation: Reynolds vs Colburn Analogy
The Reynolds analogy relates the friction factor (f) directly to the Stanton number (St) using the equation St = f/2, assuming equal eddy diffusivities for momentum and heat. The Colburn analogy refines this by introducing the Colburn j-factor, stated as j_H = St * Pr^(2/3) = f/2, incorporating the Prandtl number (Pr) to account for fluid thermal properties. This adjustment makes the Colburn analogy more accurate for heat transfer in turbulent flow by correlating convective heat transfer coefficients with friction factors through a dimensionless parameter involving Prandtl number effects.
Assumptions and Applicability
The Colburn analogy assumes turbulent flow with a constant Prandtl number, relating heat transfer and momentum transfer by incorporating a correction for the Prandtl number, making it more accurate for gases and fluids with Pr near unity. The Reynolds analogy assumes a similar turbulent flow regime but equates heat and momentum transfer directly without correcting for the Prandtl number, limiting its accuracy to fluids where Pr 1. Colburn analogy is more widely applicable to turbulent flow in pipes and channels where both heat and mass transfer are important, while Reynolds analogy is primarily used in simplified cases with unity Prandtl number and fully developed turbulent flow.
Key Differences Between Colburn and Reynolds Analogy
The Colburn analogy introduces a heat transfer factor jH to explicitly relate heat transfer to momentum transfer, enhancing accuracy for turbulent flow, while the Reynolds analogy assumes equal Stanton and friction factors, simplifying the relationship but limiting precision. Colburn's approach accounts for Prandtl number variations, providing better predictions across fluids, whereas Reynolds analogy presumes a Prandtl number of 1. Furthermore, Colburn analogy is applicable in both laminar and turbulent regimes with adjustments, whereas Reynolds analogy primarily focuses on turbulent flow with less adaptability.
Practical Applications in Engineering
The Colburn analogy is widely applied in heat exchanger design due to its ability to accurately correlate heat transfer and friction factors under turbulent flow conditions, enhancing thermal performance predictions. The Reynolds analogy simplifies the relationship between momentum and heat transfer in fluid flows, making it useful for preliminary analysis in pipe flow and duct design where mass and heat transfer are coupled. Engineers often select the Colburn analogy for detailed convective heat transfer modeling, while the Reynolds analogy serves well in cases requiring quick estimates of heat transfer coefficients.
Limitations of Each Analogy
The Colburn analogy tends to overestimate heat transfer rates in turbulent flow with high Prandtl numbers due to its simplified assumptions about velocity and thermal boundary layers. The Reynolds analogy is limited by its assumption of equal turbulent momentum and heat transfer diffusivities, which often fails in fluids with Prandtl numbers significantly different from unity. Both analogies lose accuracy in complex flow regimes, such as those with significant pressure gradients or variable fluid properties.
Summary and Conclusion
The Colburn analogy refines the Reynolds analogy by incorporating the Colburn j-factor, which accounts for variations in heat transfer and fluid flow, making it more accurate for turbulent flow conditions. Reynolds analogy assumes equal momentum and heat transfer coefficients, suitable primarily for simple laminar flow scenarios. The Colburn analogy is preferred in engineering applications due to its enhanced predictive capability for heat and mass transfer in turbulent boundary layers.
Colburn analogy Infographic
 libterm.com
libterm.com