Dimensionality reduction techniques streamline complex datasets by reducing the number of variables while preserving essential information, enhancing model performance and visualization clarity. Methods like Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE) are widely used for uncovering patterns in high-dimensional data. Explore the full article to understand how dimensionality reduction can improve Your data analysis workflows.
Table of Comparison
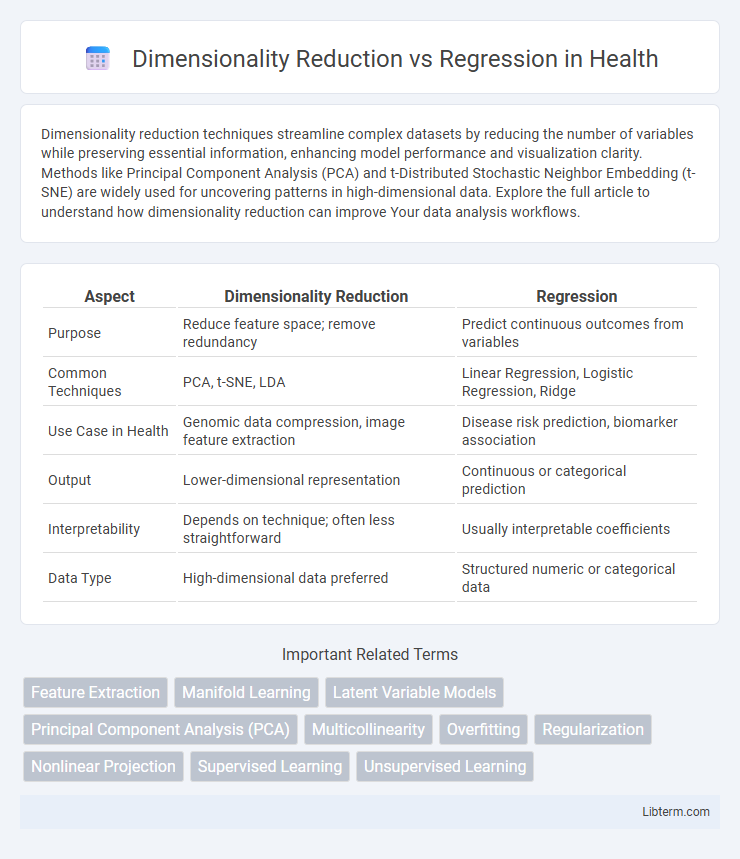
| Aspect | Dimensionality Reduction | Regression |
|---|---|---|
| Purpose | Reduce feature space; remove redundancy | Predict continuous outcomes from variables |
| Common Techniques | PCA, t-SNE, LDA | Linear Regression, Logistic Regression, Ridge |
| Use Case in Health | Genomic data compression, image feature extraction | Disease risk prediction, biomarker association |
| Output | Lower-dimensional representation | Continuous or categorical prediction |
| Interpretability | Depends on technique; often less straightforward | Usually interpretable coefficients |
| Data Type | High-dimensional data preferred | Structured numeric or categorical data |
Introduction to Dimensionality Reduction and Regression
Dimensionality reduction techniques, such as Principal Component Analysis (PCA) and t-Distributed Stochastic Neighbor Embedding (t-SNE), transform high-dimensional data into a lower-dimensional space to improve computational efficiency and visualization while preserving essential information. Regression methods, including linear regression and polynomial regression, model the relationship between independent variables and a continuous dependent variable to predict outcomes or identify trends. Both approaches are fundamental in data analysis, with dimensionality reduction enhancing feature representation and regression enabling predictive modeling.
Key Concepts: What is Dimensionality Reduction?
Dimensionality Reduction is a process in machine learning that transforms high-dimensional data into a lower-dimensional space while preserving essential information. Techniques like Principal Component Analysis (PCA) and t-SNE help in visualizing data and improving computational efficiency by reducing noise and redundancy. Unlike regression, which predicts continuous outcomes based on input features, dimensionality reduction focuses on simplifying data representation without targeting prediction tasks.
Understanding Regression Techniques
Regression techniques such as linear regression, polynomial regression, and ridge regression focus on modeling relationships between dependent and independent variables to predict continuous outcomes. Dimensionality reduction methods like Principal Component Analysis (PCA) and t-SNE aim to reduce feature space complexity by transforming data into lower dimensions while preserving variance or structure, facilitating better model performance and visualization. Understanding the distinctions helps in selecting appropriate methods for predictive accuracy and feature simplification in machine learning tasks.
Core Objectives: Reduction vs Prediction
Dimensionality reduction aims to simplify data by reducing the number of features while preserving essential information, enhancing visualization and improving computational efficiency. Regression focuses on predicting a continuous target variable based on input features, modeling the relationship to forecast outcomes accurately. Both approaches handle data complexity but serve distinct objectives: dimensionality reduction compresses data, while regression generates predictive insights.
Common Algorithms in Dimensionality Reduction
Principal Component Analysis (PCA) is a widely used dimensionality reduction algorithm that transforms data into a lower-dimensional space while preserving variance. t-Distributed Stochastic Neighbor Embedding (t-SNE) excels at visualizing high-dimensional data by modeling each high-dimensional object by a two- or three-dimensional point. Linear Discriminant Analysis (LDA) serves both as a classifier and dimensionality reduction technique by maximizing class separability in reduced dimensions.
Popular Regression Methods Explained
Popular regression methods include linear regression, which models the relationship between variables by fitting a linear equation, and support vector regression (SVR), which uses margin-based optimization for flexibility and robustness. Dimensionality reduction techniques like PCA (Principal Component Analysis) and t-SNE reduce feature space complexity to improve regression model performance by removing noise and multicollinearity. Combining dimensionality reduction with regression enhances predictive accuracy and interpretability, especially in high-dimensional datasets with numerous correlated features.
Differences in Application and Use Cases
Dimensionality reduction is primarily used to simplify large datasets by reducing features while preserving essential information, which enhances data visualization and improves model performance in tasks like clustering and anomaly detection. Regression focuses on predicting continuous outcomes based on input variables, commonly applied in forecasting, risk assessment, and trend analysis. Unlike regression, dimensionality reduction is not aimed at prediction but at optimizing datasets for better interpretability and computational efficiency in high-dimensional scenarios.
Performance Metrics: How Are They Evaluated?
Dimensionality reduction is typically evaluated through metrics such as reconstruction error, explained variance, and clustering performance, which assess how well the reduced data preserves original structure and information. Regression performance metrics include mean squared error (MSE), R-squared, and mean absolute error (MAE), focusing on the accuracy and goodness-of-fit between predicted and actual values. While dimensionality reduction is judged by its ability to maintain data integrity in fewer dimensions, regression evaluation directly measures prediction accuracy on dependent variables.
When to Use Dimensionality Reduction or Regression
Dimensionality reduction is best used when dealing with high-dimensional datasets to eliminate redundant or irrelevant features, improve model performance, and enhance visualization by reducing the number of variables while preserving essential information. Regression is appropriate when the goal is to predict a continuous target variable based on input features, modeling the relationship between dependent and independent variables to make accurate forecasts. Choose dimensionality reduction when feature extraction or data preprocessing is needed, and select regression when the primary task involves prediction or understanding variable relationships.
Conclusion: Choosing the Right Approach
Dimensionality reduction techniques like PCA are ideal for simplifying data with many features by projecting it into a lower-dimensional space, enhancing model performance and interpretability. Regression methods directly model relationships between variables, making them essential for prediction and inference tasks when the goal is understanding specific variable impacts. Selecting the right approach depends on the analysis objective: use dimensionality reduction to address multicollinearity and reduce noise, while relying on regression to quantify and predict target variable outcomes.
Dimensionality Reduction Infographic
 libterm.com
libterm.com