Linear design emphasizes simplicity and clarity by organizing elements in a straight, sequential path that guides the viewer's eye effortlessly. This approach enhances user experience by minimizing distractions and highlighting critical information, making it ideal for clear communication. Explore the full article to discover how linear design can improve your projects and capture your audience's attention effectively.
Table of Comparison
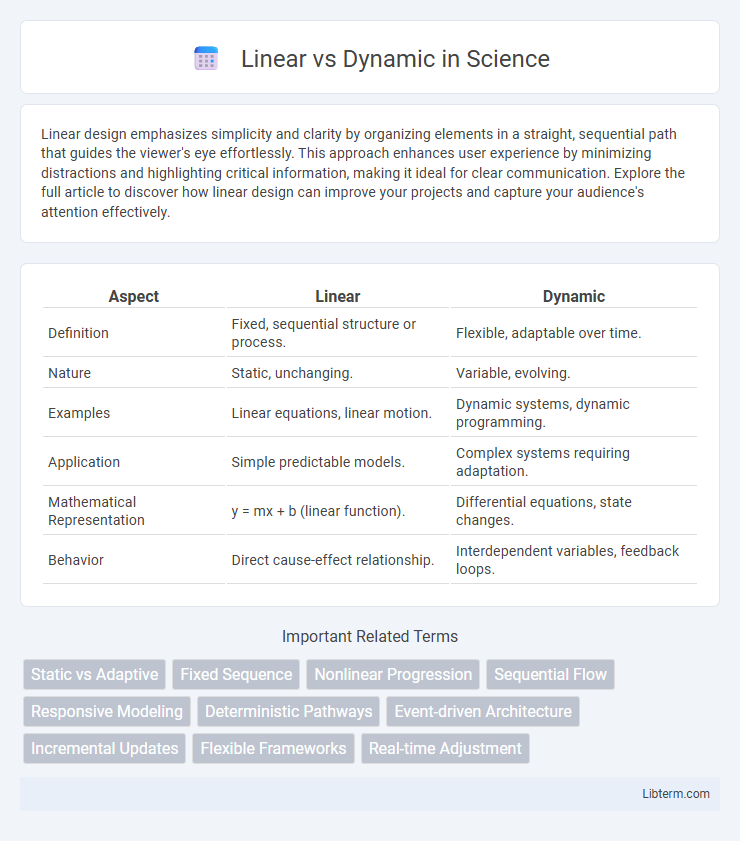
| Aspect | Linear | Dynamic |
|---|---|---|
| Definition | Fixed, sequential structure or process. | Flexible, adaptable over time. |
| Nature | Static, unchanging. | Variable, evolving. |
| Examples | Linear equations, linear motion. | Dynamic systems, dynamic programming. |
| Application | Simple predictable models. | Complex systems requiring adaptation. |
| Mathematical Representation | y = mx + b (linear function). | Differential equations, state changes. |
| Behavior | Direct cause-effect relationship. | Interdependent variables, feedback loops. |
Introduction to Linear and Dynamic Approaches
Linear approaches rely on fixed, pre-defined rules or models that follow a direct, sequential progression, making them suitable for predictable and structured environments. Dynamic approaches adapt in real-time by continuously updating models based on new data, enabling flexibility and responsiveness in complex or changing contexts. Understanding the distinction between these methods is crucial for selecting the appropriate strategy in machine learning, control systems, or data analysis tasks.
Defining Linear Methods
Linear methods involve models where the relationship between input variables and the output is expressed as a linear combination, enabling straightforward interpretation and efficient computation. These methods assume constant coefficients and additive effects, making them suitable for datasets with linear patterns. Common examples include linear regression and linear discriminant analysis, which prioritize simplicity and scalability in data modeling.
Understanding Dynamic Methods
Dynamic methods adapt behavior at runtime by resolving method calls using late binding, enabling polymorphism and flexible code execution. Unlike linear methods that follow a fixed, static call sequence, dynamic methods utilize runtime information to select appropriate implementations, enhancing extensibility and responsiveness. This approach is critical in scenarios like event handling, plugin architectures, and real-time system adjustments where adaptability is paramount.
Key Differences: Linear vs Dynamic
Linear systems operate with fixed, predictable relationships between input and output, maintaining proportionality and additivity, making them easier to model and analyze. Dynamic systems exhibit time-dependent behavior with states changing over time, often involving feedback loops and complexities such as delays and nonlinearity. The key difference lies in linear systems' static, straightforward input-output mapping versus dynamic systems' evolving, context-sensitive state changes.
Advantages of Linear Approaches
Linear approaches offer clear advantages such as simplicity, ease of implementation, and interpretability, making them ideal for problems with linear relationships. These methods typically require less computational power and can efficiently handle large datasets with consistent patterns. Their straightforward nature allows for easier debugging and model tuning, ensuring faster deployment and reliable predictions.
Benefits of Dynamic Strategies
Dynamic strategies offer enhanced flexibility and adaptability by continuously adjusting to changing market conditions, leading to improved risk management and optimized resource allocation. They enable real-time data analysis to make informed decisions, increasing responsiveness and competitive advantage in volatile environments. Unlike linear approaches, dynamic strategies support scalable growth and innovation by evolving with business needs and external factors.
Use Cases: When to Choose Linear
Linear workflows excel in projects with predictable, sequential steps such as manufacturing processes or software development phases where tasks follow a strict order. Dynamic workflows suit environments requiring flexibility, like customer support or marketing campaigns, where task priorities shift frequently. Choose linear when clarity, consistency, and repeatability are crucial to minimize errors and ensure timely delivery.
Use Cases: When to Choose Dynamic
Dynamic systems excel in use cases requiring adaptability to changing environments, such as real-time data processing, adaptive control systems, and machine learning applications. They handle nonlinear behaviors and uncertainties effectively, making them ideal for robotics, autonomous vehicles, and personalized recommendation engines. Choosing dynamic models suits scenarios where flexibility and responsiveness to fluctuating inputs are critical for performance and accuracy.
Challenges and Limitations
Linear systems face challenges such as limited adaptability and inability to handle non-linear behaviors, restricting their use in complex real-world scenarios. Dynamic systems encounter difficulties related to stability, parameter estimation, and computational complexity, which can impede real-time processing and accurate modeling. Both approaches require careful consideration of system dynamics to optimize performance and minimize errors in practical applications.
Conclusion: Selecting the Right Approach
Choosing between linear and dynamic models depends on the complexity and variability of the task at hand. Linear models are efficient and interpretable for problems with consistent, predictable patterns, while dynamic models excel in handling time-dependent or rapidly changing data. Evaluating the specific requirements, data structure, and desired outcome is crucial to selecting the most effective approach.
Linear Infographic
 libterm.com
libterm.com