Contour enhances facial features by defining and sculpting natural lines, creating dimension and depth for a flawless look. Using the right contour techniques and products can transform your makeup routine, highlighting your best attributes with subtle shadows and highlights. Discover the most effective contouring tips and tricks to elevate your beauty game in the rest of this article.
Table of Comparison
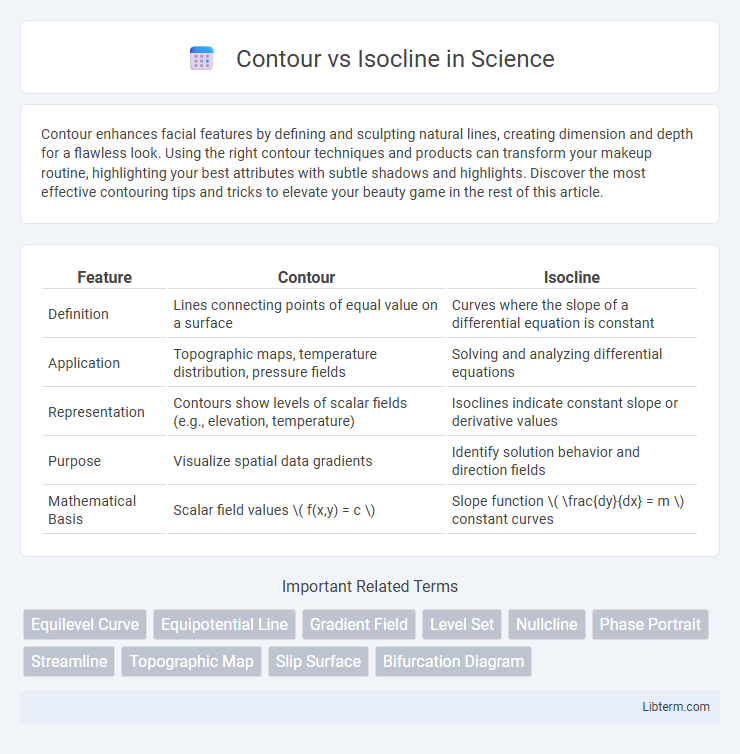
| Feature | Contour | Isocline |
|---|---|---|
| Definition | Lines connecting points of equal value on a surface | Curves where the slope of a differential equation is constant |
| Application | Topographic maps, temperature distribution, pressure fields | Solving and analyzing differential equations |
| Representation | Contours show levels of scalar fields (e.g., elevation, temperature) | Isoclines indicate constant slope or derivative values |
| Purpose | Visualize spatial data gradients | Identify solution behavior and direction fields |
| Mathematical Basis | Scalar field values \( f(x,y) = c \) | Slope function \( \frac{dy}{dx} = m \) constant curves |
Definition of Contour and Isocline
Contour lines represent curves connecting points of equal value of a specific variable, such as elevation or temperature, on a map or graph, illustrating spatial variations. Isoclines are lines on a differential equation graph where the slope of the solution curve is constant, helping to visualize the direction field and analyze system behavior. Both contours and isoclines serve as essential tools in mathematical and scientific visualization for interpreting complex data patterns.
Key Differences Between Contour and Isocline
Contour lines represent points of equal elevation on a map, illustrating the topography of a landscape by connecting locations with the same height above sea level. Isoclines, on the other hand, are curves on a graph or map where a differential equation's slope is constant, helping to visualize the direction fields in differential equations. The key difference lies in their application and meaning: contours describe physical terrain elevation, while isoclines describe mathematical slope behavior in dynamic systems.
Applications in Geography and Ecology
Contour lines represent elevation or depth on maps, enabling detailed terrain analysis essential for geographic information systems and landscape planning. Isoclines, indicating regions of equal slope or gradient, assist ecologists in understanding species distribution patterns influenced by environmental factors like soil moisture and sunlight exposure. Both tools facilitate habitat modeling and resource management by providing spatial insights into topographical and ecological variations.
Mathematical Representation of Contours
Contours represent curves on a graph where a function of two variables remains constant, typically expressed as f(x, y) = k, illustrating levels of equal value. Isoclines, in contrast, are curves in differential equations where the slope dy/dx equals a constant m, defined by the equation dy/dx = m, indicating lines of constant slope. The mathematical representation of contours involves setting the function equal to fixed constants to visualize behavior across a domain, essential for interpreting gradient fields and potential surfaces in multivariable calculus.
Mathematical Representation of Isoclines
Isoclines are curves representing points where a given differential equation has a constant slope, defined by the equation dy/dx = f(x, y) = m, where m is a fixed value. Mathematically, isoclines solve f(x, y) = m for y, providing a family of curves that help visualize the direction field of the differential equation. Contours, in contrast, depict level sets of a function z = g(x, y) where g(x, y) = c, focusing on values rather than slopes.
Visualization Techniques for Contour Lines
Contour lines represent constant values on a graph and are essential in topographic maps for depicting elevation, while isoclines connect points of equal slope or rate of change in differential equations. Visualization techniques for contour lines include color gradients to illustrate elevation changes, smoothing algorithms to enhance line clarity, and interactive layering to distinguish multiple contour levels effectively. Advanced tools use 3D rendering and dynamic scaling to improve spatial understanding and precision in representing complex surfaces.
Visualization Techniques for Isoclines
Isoclines are visualized using curve plots that represent points where the differential equation exhibits a constant slope, enabling the analysis of solution behaviors without solving the equation explicitly. Visualization techniques for isoclines often employ vector fields or slope fields, where tangent lines are drawn at grid points to indicate the direction of solutions, facilitating intuitive comprehension of dynamic systems. These graphical methods contrast with contour plots, which depict level sets of scalar functions, emphasizing the role of isoclines in differential equation phase-plane analysis.
Importance in Field Studies and Modeling
Contour lines represent constant values of a variable across a geographical area, crucial for visualizing spatial patterns in field studies such as topography, temperature, or pollution levels. Isoclines, defining locations where the rate of change in a differential equation remains constant, are vital in modeling dynamic systems like population growth or chemical reactions, helping to predict system behavior under varying conditions. Both tools provide essential insights by translating complex data into interpretable visual formats, enhancing accuracy in environmental analysis and predictive modeling.
Common Mistakes in Interpreting Contours and Isoclines
Misinterpreting contours as isoclines often leads to confusion in analyzing differential equations because contours represent levels of a function whereas isoclines indicate curves where the slope of the solution is constant. A common mistake is treating contour lines as directional indicators of the solution trajectories instead of understanding that isoclines help sketch direction fields for differential equations. Accurate interpretation requires recognizing contours define function values while isoclines assist in visualizing slope behavior, thus avoiding incorrect conclusions in dynamic systems analysis.
Summary: Choosing the Right Tool for Analysis
Contour lines represent continuous levels of a variable on a map, ideal for visualizing gradients and spatial distributions, while isoclines depict points of equal slope or rate of change in differential equations, crucial for understanding system behavior. Selecting between contour and isocline analysis depends on whether the goal is to interpret spatial variation or dynamic system stability. For accurate modeling and interpretation, use contour maps in geographic or physical data visualization and isoclines in mathematical or ecological growth studies.
Contour Infographic
 libterm.com
libterm.com