An isoquant represents a curve depicting all combinations of two inputs that produce the same level of output in production. Understanding isoquants allows you to analyze how changes in input quantities affect production efficiency and cost optimization. Explore the rest of the article to learn how isoquants can improve your decision-making in resource allocation.
Table of Comparison
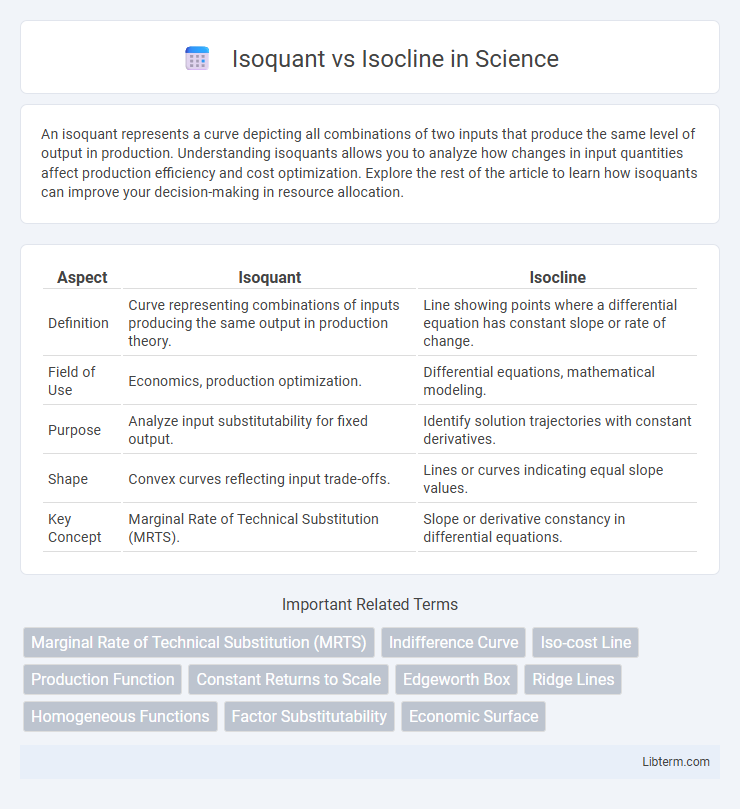
| Aspect | Isoquant | Isocline |
|---|---|---|
| Definition | Curve representing combinations of inputs producing the same output in production theory. | Line showing points where a differential equation has constant slope or rate of change. |
| Field of Use | Economics, production optimization. | Differential equations, mathematical modeling. |
| Purpose | Analyze input substitutability for fixed output. | Identify solution trajectories with constant derivatives. |
| Shape | Convex curves reflecting input trade-offs. | Lines or curves indicating equal slope values. |
| Key Concept | Marginal Rate of Technical Substitution (MRTS). | Slope or derivative constancy in differential equations. |
Introduction to Isoquant and Isocline
Isoquants represent curves on a graph that depict combinations of inputs producing the same level of output in production theory, essential for understanding efficient resource allocation in economics. Isoclines, in contrast, are lines on a phase plane indicating points where the slope of a differential equation remains constant, used primarily in the analysis of dynamic systems and stability in mathematical modeling. Both concepts involve curves illustrating constant values but apply in distinct contexts: isoquants relate to production functions, while isoclines concern differential equations.
Fundamental Concepts: Isoquant Explained
Isoquants represent combinations of different inputs, such as labor and capital, that produce the same level of output, illustrating the trade-offs in production processes without changing output quantity. These curves are fundamental in production theory for analyzing how firms can substitute one input for another while maintaining constant production. Isoquants differ from isoclines, which are used in differential equations to depict points where the slope of a curve is constant, highlighting their distinct roles in economics and mathematics.
Understanding Isocline: Definition and Importance
Isoclines are curves representing points where a differential equation has the same slope, crucial for analyzing and visualizing solution behaviors in mathematical modeling. Understanding isoclines helps in constructing direction fields and predicting the dynamics of systems without solving the equation explicitly. This concept is vital in fields like economics and biology for interpreting system stability and growth patterns.
Mathematical Representation of Isoquant
The mathematical representation of an isoquant is a function \( f(L, K) = Q \), where \( L \) and \( K \) denote quantities of labor and capital, respectively, and \( Q \) represents a fixed output level. Isoquants are contour lines of the production function, illustrating combinations of inputs yielding constant production. Unlike isoclines used in differential equations to show slopes, isoquants specifically map input combinations in production theory for a given output.
Mathematical Representation of Isocline
Isoclines are curves in differential equations representing points where the slope of the solution curve is constant, defined mathematically by setting dy/dx = m to find lines or curves with slope m. In contrast, isoquants in economics graphically depict production functions where output remains constant for varying inputs. The mathematical representation of an isocline involves solving the differential equation for dy/dx = f(x,y) = m, yielding a family of isoclines used to analyze solution behavior.
Key Differences Between Isoquant and Isocline
Isoquant represents combinations of inputs that produce the same level of output in production theory, while isocline refers to curves showing points of equal slope in differential equations. Key differences include their application--isoquants are used in microeconomics to analyze input-output relationships, whereas isoclines are applied in mathematical modeling to study slope fields and solutions of differential equations. Isoquants focus on production efficiency, whereas isoclines emphasize changes in rates of change or gradients in a system.
Applications of Isoquants in Economics
Isoquants are widely used in economics to analyze production efficiency by illustrating combinations of input factors like labor and capital that yield the same output level, facilitating optimal resource allocation in firms. They help businesses identify the least-cost input mix and evaluate the marginal rate of technical substitution between inputs. In contrast, isoclines primarily appear in differential equations and have limited direct application in economic production analysis.
Applications of Isoclines in Mathematics and Ecology
Isoclines serve crucial roles in mathematics and ecology by representing curves along which a differential equation has constant slope, aiding in the qualitative analysis of dynamic systems. In ecological modeling, isoclines help predict population stability by indicating points where species' growth rates change, facilitating the study of predator-prey interactions and competition models. Unlike isoquants, which illustrate combinations of inputs yielding equal output in economics, isoclines focus on system behavior in phase planes, making them essential for stability analysis and understanding equilibrium points.
Graphical Analysis: Isoquant vs Isocline
Isoquants graphically represent combinations of inputs that yield the same level of output, typically displayed as smooth convex curves in production theory. Isoclines, on the other hand, are lines in differential equation analysis where the slope of the solution curve remains constant, often used to identify equilibrium directions on phase planes. The isoquant focuses on input substitution in economics, while the isocline emphasizes geometric properties of differential equations.
Conclusion: Choosing Between Isoquant and Isocline
Isoquants represent combinations of inputs producing the same output, essential for analyzing production efficiency and optimal resource allocation. Isoclines depict locations with equal slope or growth rate in differential equations, primarily used in dynamic system behavior and stability analysis. Selecting between isoquants and isoclines depends on the context: use isoquants for production and input-output optimization, and isoclines for studying equilibrium and phase plane dynamics.
Isoquant Infographic
 libterm.com
libterm.com