Relativistic effects become significant when objects approach the speed of light, altering the classical Newtonian predictions of motion and energy. These phenomena impact time dilation, length contraction, and mass-energy equivalence, fundamentally changing our understanding of physics at high velocities. Explore the full article to uncover how relativistic principles shape modern science and technology.
Table of Comparison
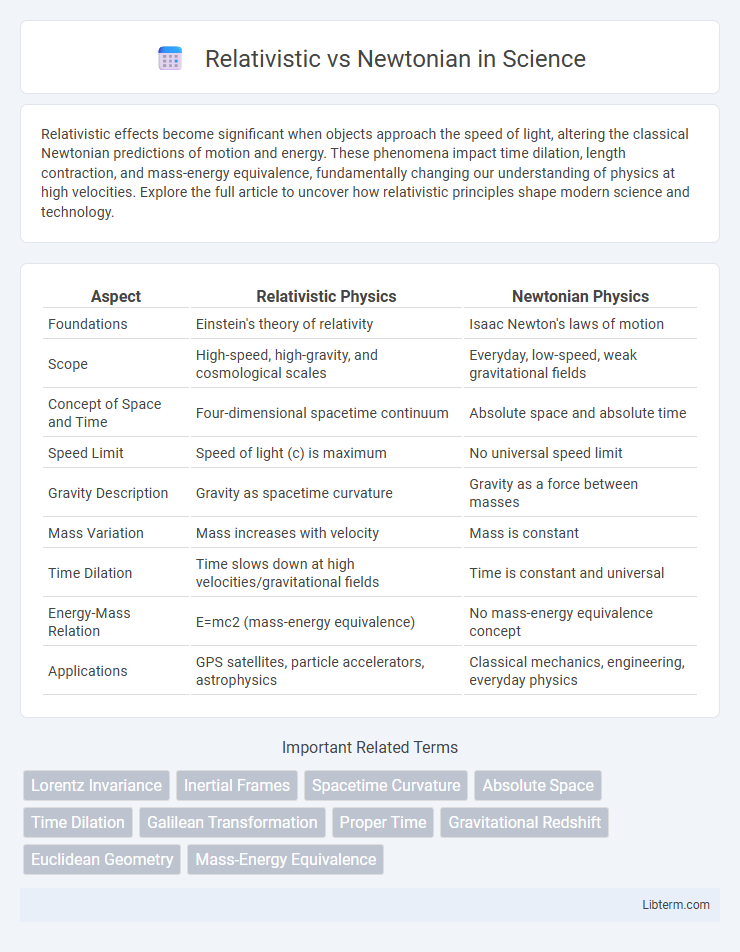
| Aspect | Relativistic Physics | Newtonian Physics |
|---|---|---|
| Foundations | Einstein's theory of relativity | Isaac Newton's laws of motion |
| Scope | High-speed, high-gravity, and cosmological scales | Everyday, low-speed, weak gravitational fields |
| Concept of Space and Time | Four-dimensional spacetime continuum | Absolute space and absolute time |
| Speed Limit | Speed of light (c) is maximum | No universal speed limit |
| Gravity Description | Gravity as spacetime curvature | Gravity as a force between masses |
| Mass Variation | Mass increases with velocity | Mass is constant |
| Time Dilation | Time slows down at high velocities/gravitational fields | Time is constant and universal |
| Energy-Mass Relation | E=mc2 (mass-energy equivalence) | No mass-energy equivalence concept |
| Applications | GPS satellites, particle accelerators, astrophysics | Classical mechanics, engineering, everyday physics |
Introduction to Relativistic and Newtonian Physics
Relativistic physics, founded on Einstein's theory of relativity, describes the behavior of objects moving at speeds close to the speed of light, where time dilation and length contraction become significant, contrasting sharply with Newtonian physics, which assumes absolute time and space and accurately explains most everyday phenomena at low velocities. Newtonian mechanics, formulated by Isaac Newton, relies on classical laws of motion and gravity that remain valid for slower speeds and weak gravitational fields. Understanding the fundamental differences between these frameworks is essential for accurately modeling physical systems ranging from planetary motion to high-energy particle collisions.
Historical Development of Classical and Modern Theories
Classical Newtonian mechanics, formulated in the 17th century by Isaac Newton, established the foundational laws of motion and universal gravitation that dominated scientific thought for over two centuries. The early 20th century ushered in the rise of relativistic physics, primarily through Albert Einstein's theories of special relativity (1905) and general relativity (1915), which redefined concepts of space, time, and gravity at high velocities and in strong gravitational fields. This historical shift from Newtonian absolutes to relativistic frameworks marked the transition from classical to modern physics, profoundly impacting theoretical and applied sciences.
Fundamental Principles: Newtonian Mechanics
Newtonian mechanics is based on three fundamental principles: the law of inertia, the law of acceleration, and the law of action and reaction. These principles assume absolute time and space, where objects move at velocities much less than the speed of light, allowing the use of classical equations of motion. Unlike relativistic mechanics, Newtonian mechanics treats mass as constant and independent of an object's velocity.
Core Concepts of Einstein’s Relativity
Einstein's relativity centers on the invariance of the speed of light and the relativity of simultaneity, fundamentally challenging Newtonian absolute space and time. The theory introduces time dilation and length contraction, showing that measurements vary depending on the observer's relative velocity. Mass-energy equivalence, expressed as E=mc2, redefines concepts of mass and energy, unifying them within a relativistic framework.
Mathematical Differences in Describing Motion
Relativistic mechanics formulates motion using Lorentz transformations, which account for the invariance of the speed of light and time dilation, modifying velocity addition and momentum equations compared to classical Newtonian mechanics. Newtonian motion relies on Galilean transformations and assumes absolute time and space, with straightforward linear equations of motion like F=ma, applicable at speeds much lower than the speed of light. Relativity introduces factors such as gamma (g), the Lorentz factor, which scales time, length, and mass, fundamentally altering the mathematical description of high-velocity motion beyond the Newtonian regime.
Time and Space: Absolute vs. Relative
Newtonian physics treats time and space as absolute, fixed entities existing independently of observers, where time flows uniformly and space is a constant stage for events. Relativistic physics, based on Einstein's theories, reveals that time and space are relative, intertwined in a four-dimensional spacetime fabric that varies with the observer's velocity and gravitational field. Experiments such as time dilation in high-speed particles and gravitational lensing confirm that measurements of time intervals and spatial distances depend on the reference frame, challenging the absolute notions of classical mechanics.
Applicability: When to Use Each Framework
Relativistic mechanics becomes essential for accurately describing phenomena at velocities close to the speed of light or in strong gravitational fields, such as particle accelerators and astrophysical contexts. Newtonian mechanics remains highly effective for everyday scenarios involving low speeds and weak gravitational forces, like engineering calculations, vehicle motion, and planetary orbits within the solar system. Choosing between frameworks depends on the velocity scale and gravitational intensity, with relativistic models providing precise results in extreme conditions where Newtonian assumptions break down.
Experimental Evidence and Observational Proof
Experiments such as the Michelson-Morley experiment and observations of time dilation in particle accelerators provide strong evidence supporting relativistic physics over Newtonian mechanics. Precise measurements of Mercury's perihelion precession and gravitational lensing during solar eclipses confirm predictions made by Einstein's theory of relativity rather than Newtonian gravity. Observational data from GPS satellite systems also require relativistic corrections, demonstrating the limitations of Newtonian models in accurately describing high-speed and strong gravitational environments.
Real-world Examples: From Satellites to Black Holes
Satellites orbiting Earth rely on relativistic corrections from Einstein's theory of General Relativity to maintain precise GPS calculations, as Newtonian mechanics alone fails to account for time dilation effects caused by gravity. In contrast, Newtonian physics accurately predicts the motion of planets in the solar system under typical gravitational conditions but cannot describe extreme phenomena such as black holes, where spacetime curvature dominates. Black holes demonstrate relativistic effects like event horizons and gravitational time dilation, which are beyond the scope of classical Newtonian gravity, highlighting the necessity of relativistic models in high-gravity environments.
Future Implications and The Unifying Quest
Relativistic physics, grounded in Einstein's theories, revolutionizes our understanding of spacetime and predicts phenomena such as time dilation and gravitational waves, driving advancements in GPS technology and quantum computing. Newtonian mechanics, while foundational for classical mechanics, faces limitations in high-velocity or strong-gravity contexts, prompting the scientific community to pursue a unified theory encompassing both quantum mechanics and general relativity. The quest for unification, embodied in approaches like string theory and loop quantum gravity, holds profound implications for future technologies, potentially enabling breakthroughs in energy, space travel, and the fundamental nature of reality.
Relativistic Infographic
 libterm.com
libterm.com