Collinear points lie on the same straight line, making them essential in geometry and coordinate systems for understanding alignment and linear relationships. Identifying collinearity helps solve problems involving distances, slopes, and equations of lines, which are fundamental in fields such as engineering and computer graphics. Discover how mastering collinear concepts can enhance your analytical skills by reading the rest of this article.
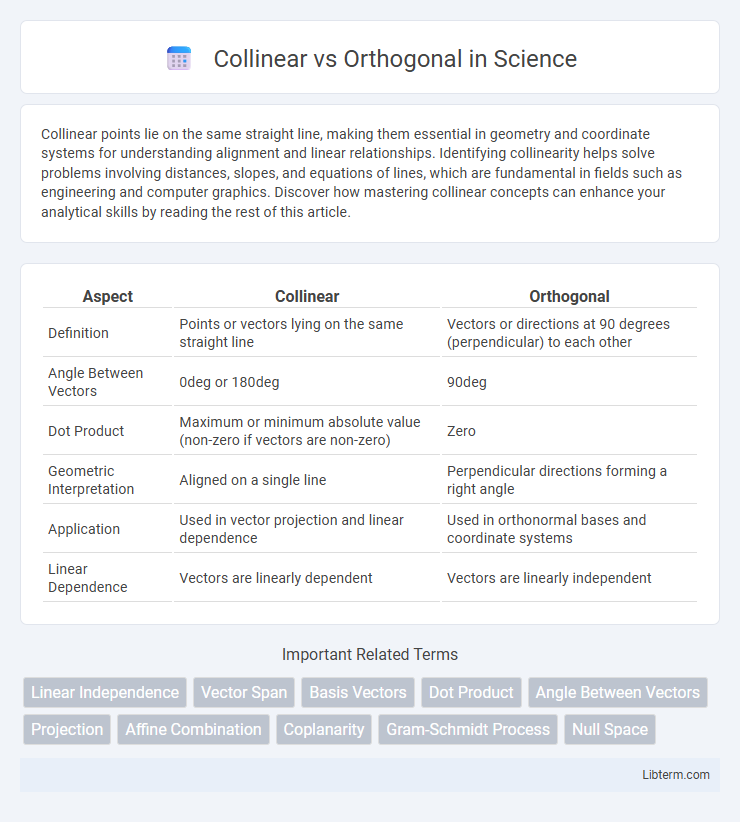
Table of Comparison
| Aspect | Collinear | Orthogonal |
|---|---|---|
| Definition | Points or vectors lying on the same straight line | Vectors or directions at 90 degrees (perpendicular) to each other |
| Angle Between Vectors | 0deg or 180deg | 90deg |
| Dot Product | Maximum or minimum absolute value (non-zero if vectors are non-zero) | Zero |
| Geometric Interpretation | Aligned on a single line | Perpendicular directions forming a right angle |
| Application | Used in vector projection and linear dependence | Used in orthonormal bases and coordinate systems |
| Linear Dependence | Vectors are linearly dependent | Vectors are linearly independent |
Introduction to Collinear and Orthogonal Concepts
Collinear points lie on a single straight line, sharing the same linear alignment, which is fundamental in both geometry and vector analysis. Orthogonal vectors or lines intersect at right angles (90 degrees), often representing perpendicular directions in Euclidean space. Understanding these concepts is crucial for applications in physics, computer graphics, and data analysis where spatial relationships define system behavior.
Defining Collinear Structures
Collinear structures refer to points or vectors that lie along the same straight line, sharing a common linear path in a coordinate system. These structures are defined by the scalar multiplication relationship between vectors, indicating that one vector can be expressed as a multiple of another. Understanding collinearity is essential in geometry and vector algebra for solving linear equations, projecting points, and detecting alignment in spatial data.
Understanding Orthogonal Relationships
Orthogonal relationships in mathematics and statistics refer to variables or vectors that are uncorrelated and independent, having a zero inner product, which ensures no linear dependency between them. Understanding these relationships is crucial for dimensionality reduction, optimization, and multivariate analysis, as orthogonality preserves the uniqueness and interpretability of features in models. Unlike collinear variables that are linearly dependent and can distort statistical inferences, orthogonal components provide clarity by maintaining independent axes in data representation and signal processing.
Key Differences Between Collinear and Orthogonal
Collinear vectors lie along the same line, meaning their direction ratios are proportional, whereas orthogonal vectors are perpendicular, having a zero dot product indicating a 90-degree angle between them. Collinearity implies linear dependence, meaning one vector can be expressed as a scalar multiple of the other, while orthogonality ensures linear independence. These fundamental differences play a crucial role in vector space applications such as physics, computer graphics, and linear algebra.
Mathematical Representation: Collinearity vs Orthogonality
Collinearity in mathematics is represented by vectors having a scalar multiple relationship, expressed as v = k*u, where vectors v and u lie on the same line or direction, and k is a scalar. Orthogonality is defined by the dot product of two vectors being zero, u * v = 0, indicating perpendicularity and no directional overlap. These mathematical conditions distinctly characterize geometric alignment: collinearity implies directional proportionality, while orthogonality signifies zero directional correlation.
Real-world Applications of Collinear Systems
Collinear systems, where vectors lie along the same line, are widely used in fields like robotics for linear motion control and in electrical engineering for signal processing along a single axis. In telecommunications, collinear antenna arrays enhance signal strength and directionality, improving data transmission efficiency. These real-world applications leverage the predictability and simplicity of collinear vector alignment to optimize performance and reliability in various technologies.
Real-world Applications of Orthogonal Systems
Orthogonal systems find widespread use in real-world applications such as wireless communication, where orthogonal frequency-division multiplexing (OFDM) enhances signal clarity and bandwidth efficiency by minimizing interference between channels. In image processing, orthogonal transformations like the discrete cosine transform (DCT) optimize data compression by separating image components into uncorrelated basis functions. Engineering disciplines utilize orthogonal systems in control theory and signal processing to design stable, efficient algorithms for filtering, modulation, and noise reduction.
Advantages and Limitations of Collinear Arrangements
Collinear arrangements in antenna design offer significant advantages such as increased gain and improved directivity by stacking multiple antenna elements vertically. These configurations enhance signal strength and range, making them ideal for long-distance communication. However, collinear arrays can face limitations including increased physical height, structural complexity, and potential issues with mutual coupling between elements that may affect performance.
Benefits and Challenges of Orthogonal Configurations
Orthogonal configurations offer increased signal isolation and reduced interference due to their perpendicular element arrangement, enhancing overall system performance in complex environments. This design improves spatial diversity and minimizes correlation, benefiting applications such as MIMO antenna systems and multi-axis sensors. Challenges include increased physical space requirements and potential complexity in design and installation compared to collinear setups.
Choosing Between Collinear and Orthogonal Approaches
Choosing between collinear and orthogonal approaches depends on the specific application requirements and desired data separation. Collinear design emphasizes alignment along the same axis, enhancing signal strength and simplifying integration, while orthogonal design ensures independence between components or variables, reducing interference and improving overall system robustness. Evaluating factors such as spatial constraints, noise tolerance, and data interpretation clarity assists in determining the optimal method for system design or data analysis.
Collinear Infographic
 libterm.com
libterm.com