Arc is a cutting-edge web browser designed to enhance your online experience with a sleek interface and powerful customization options. It offers integrated tools for productivity, privacy, and seamless navigation across devices. Explore the rest of this article to discover how Arc can transform the way you browse the internet.
Table of Comparison
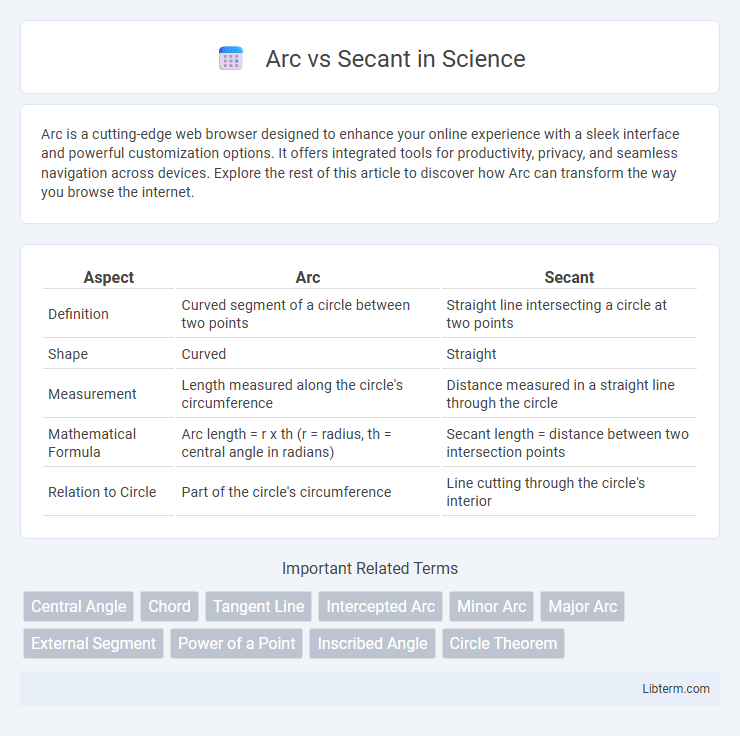
| Aspect | Arc | Secant |
|---|---|---|
| Definition | Curved segment of a circle between two points | Straight line intersecting a circle at two points |
| Shape | Curved | Straight |
| Measurement | Length measured along the circle's circumference | Distance measured in a straight line through the circle |
| Mathematical Formula | Arc length = r x th (r = radius, th = central angle in radians) | Secant length = distance between two intersection points |
| Relation to Circle | Part of the circle's circumference | Line cutting through the circle's interior |
Introduction to Arc and Secant
Arc represents a portion of the circumference of a circle, defined by two points on the circle's edge, and is measured in degrees or radians. Secant is a straight line that intersects a circle at two distinct points, extending beyond the circle's boundary. Understanding the differences between arc length and secant line segment helps in solving geometric and trigonometric problems related to circles.
Definitions: Arc and Secant Explained
An arc is a continuous portion of the circumference of a circle, defined by two points on the circle and the curved path connecting them. A secant is a straight line that intersects a circle at exactly two distinct points, cutting through its interior. Understanding the key difference between the curved nature of an arc and the linear nature of a secant is fundamental in geometry and trigonometry.
Geometric Significance of Arcs
The geometric significance of arcs lies in their representation as continuous segments of a circle's circumference, defined by central angles measured in radians or degrees. Unlike secants, which are straight lines intersecting the circle at two points, arcs capture the curved distance between these points along the circle's boundary, essential for understanding sector areas and angular displacement in trigonometry. This distinction highlights arcs as fundamental elements for calculating precise angle measures and arc lengths in geometric and analytical applications.
Understanding Secants in Circles
A secant in a circle is a straight line that intersects the circle at exactly two points, extending infinitely in both directions. Unlike an arc, which is a curved segment of the circle's circumference between two points, the secant passes through the circle, creating two intersection points on the circle's boundary. Understanding secants is essential for solving problems related to chord lengths, angle measures formed by intersecting secants, and various circle theorems.
Key Differences Between Arc and Secant
An arc is a continuous curved portion of the circumference of a circle, whereas a secant is a straight line that intersects a circle at two points. Arcs measure the distance along the circle's curve between two points, typically expressed in degrees or radians, while secants represent linear segments that pass through the circle extending beyond its boundary. The fundamental difference lies in the arc being a curved path on the circle, contrasted with the secant being a straight line cutting through it.
Mathematical Formulas Involving Arcs
The arc length formula \( s = r\theta \) relates the radius \(r\) and central angle \(\theta\) in radians to the length of the arc, essential in circle geometry. The secant function, expressed as \( \sec \theta = \frac{1}{\cos \theta} \), connects directly with trigonometric calculations involving angles on the unit circle. Inverse trigonometric functions like \( \arccos x \) or \( \arcsec x \) find angles corresponding to cosine and secant values, vital for solving equations involving arcs and segments of circles or sectors in advanced mathematics.
Secant Properties and Theorems
The secant line intersects a circle at two distinct points, extending beyond the circle's circumference. Key properties include the Secant-Secant Theorem, which states that the product of the segments of one secant equals the product of the segments of another secant drawn from the same external point. This theorem is fundamental in solving geometric problems involving circle secants and their segment lengths.
Applications of Arc and Secant in Real Life
Arc length is essential in designing curved structures like roads, bridges, and roller coasters, ensuring accurate measurements for safety and aesthetics. Secant lines are crucial in fields like astronomy and geography for calculating distances and angles when observing celestial bodies or mapping terrains. Both arcs and secants enable precise modeling in engineering, physics, and navigation, enhancing real-world problem-solving and spatial analysis.
Arc and Secant in Trigonometry
Arc in trigonometry refers to a segment of a circle's circumference subtended by a central angle, measured in degrees or radians. The secant function, sec(th), is the reciprocal of the cosine function and represents the ratio of the hypotenuse to the adjacent side in a right triangle. Understanding the relationship between arcs and the secant function helps in solving problems involving circular motion, wave patterns, and angular measurements.
Summary: Arc vs Secant Comparison
Arc represents the curved portion of a circle's circumference between two points, measured along the curve, while a secant is a straight line that intersects the circle at two points. Arcs are quantified by their length or central angle, whereas secants are identified by their linear distance and chord properties. Understanding the distinction between arc length and secant line segment is essential for solving geometric problems involving circles.
Arc Infographic
 libterm.com
libterm.com