A chord is a fundamental element of music consisting of three or more notes played simultaneously, creating harmony and mood in a composition. Understanding chord structures and progressions enhances your ability to play, compose, and appreciate music across genres. Explore the rest of this article to deepen your knowledge of chords and improve your musical skills.
Table of Comparison
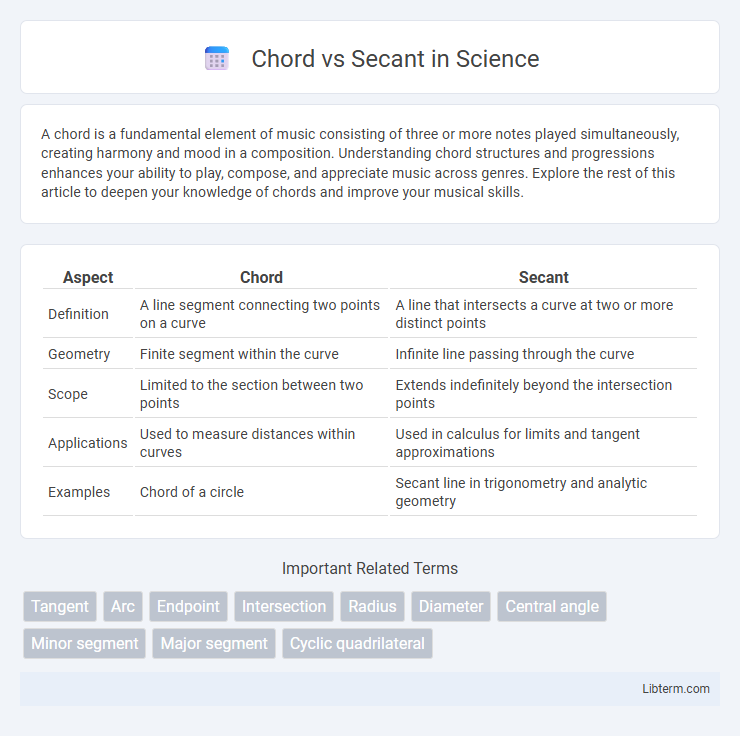
| Aspect | Chord | Secant |
|---|---|---|
| Definition | A line segment connecting two points on a curve | A line that intersects a curve at two or more distinct points |
| Geometry | Finite segment within the curve | Infinite line passing through the curve |
| Scope | Limited to the section between two points | Extends indefinitely beyond the intersection points |
| Applications | Used to measure distances within curves | Used in calculus for limits and tangent approximations |
| Examples | Chord of a circle | Secant line in trigonometry and analytic geometry |
Introduction to Chord and Secant
A chord is a line segment connecting two points on a circle, creating a shortcut across the circle's interior, while a secant is an extended line intersecting the circle at two points, passing through its interior and beyond. Chords are fundamental in circle geometry for defining arcs and segments, whereas secants relate to angles formed outside the circle and are crucial in theorems involving circle intersections. Understanding the distinction between chords and secants is essential for solving problems in trigonometry, coordinate geometry, and circle theorems.
Definitions: Chord and Secant
A chord is a line segment with both endpoints lying on the circumference of a circle, creating a direct connection between two points on the curve. A secant extends beyond a chord by continuing as a line that intersects the circle at exactly two points, effectively cutting through the circle. Understanding the difference between a chord and a secant is fundamental in geometry for analyzing circle properties and solving related problems.
Key Differences Between Chord and Secant
A chord is a line segment with both endpoints on the circle, while a secant is a line that intersects the circle at exactly two points, extending infinitely in both directions. Chords are finite with fixed length inside the circle, whereas secants extend beyond the circle's boundary. The primary difference lies in chords being segments and secants being lines that pass through the circle.
Geometric Properties of a Chord
A chord is a straight line segment joining two points on a circle, dividing it into two arcs, while a secant intersects the circle at two points and extends beyond the circumference. The geometric properties of a chord include its perpendicular bisector passing through the circle's center, and the fact that equal chords subtend equal angles at the center. The length of a chord is directly related to the radius and the central angle it subtends, calculated using the formula \( \text{Chord Length} = 2r \sin(\theta/2) \), where \( r \) is the radius and \( \theta \) the central angle.
Geometric Properties of a Secant
A secant is a line that intersects a circle at two distinct points, extending beyond the circle in both directions, while a chord is a segment connecting those intersection points within the circle. Geometrically, the secant's extension allows it to form angles with tangent lines and other secants, enabling the use of secant-secant angle theorems in circle geometry. The secant's external segment length and internal chord length relate through the Power of a Point theorem, highlighting its critical role in advanced geometric constructions and proofs.
Formulas Related to Chords
Chord formulas involve the calculation of chord length using the radius and the subtended central angle, represented as \(c = 2r \sin(\theta/2)\), where \(c\) is the chord length, \(r\) is the radius, and \(\theta\) is the central angle in radians. In contrast, secant lines intersect a circle at two points but extend infinitely beyond them, and their length between intersection points relates to the power of a point theorem \(PA \times PB = PC \times PD\). Understanding the chord formula provides a direct way to calculate distances inside a circle, while the secant formula involves external segment lengths crucial for solving problems in circle geometry.
Formulas Related to Secants
Secants involve lines intersecting a circle at two distinct points, with the secant segment lengths related by the Secant Segment Theorem: if two secants, \( PA \) and \( PB \), extend from an external point \( P \) intersecting the circle at points \( A, B \) and \( C, D \), then \( PA \times PB = PC \times PD \). The exterior segment \( PE \) of a secant and its entire length satisfy the formula \( PE \times PT = PF^2 \), where \( PF \) is the tangent length if one secant degenerates into a tangent. Understanding these formulas clarifies the relationship between distances along secants intersecting circles.
Real-life Applications of Chord and Secant
Chords are widely used in architectural design and engineering to determine the stability and load distribution in curved structures like arches and bridges. Secants find practical application in astronomy and navigation, where they help calculate distances and angles between celestial objects or landmarks by intersecting circles and curves. Both concepts play crucial roles in computer graphics for rendering curves and in trigonometric measurements for precise location mapping.
Common Misconceptions
A common misconception about chords and secants is that they are interchangeable terms; however, a chord is a line segment with both endpoints on the circle, while a secant is a line that intersects the circle at two points and extends infinitely in both directions. Many learners confuse the finite nature of chords with the infinite extension of secants, overlooking that chords lie entirely within the circle's boundary. Understanding this distinction is crucial when solving geometric problems involving circle theorems and properties.
Summary: Chord vs Secant
The chord is a line segment connecting two points on a curve, while the secant extends infinitely in both directions through those points. In geometry, chords are finite and lie entirely within the circle, whereas secants intersect the circle at two points and continue beyond. Understanding the distinction is essential in calculus and trigonometry for analyzing curves and angles.
Chord Infographic
 libterm.com
libterm.com