Diameter is the straight line passing through the center of a circle, connecting two points on its circumference, and it is twice the length of the radius. Understanding the diameter is essential for calculating circumference, area, and many geometric properties of circles and spheres. Explore the rest of this article to deepen your grasp of diameter and its practical applications.
Table of Comparison
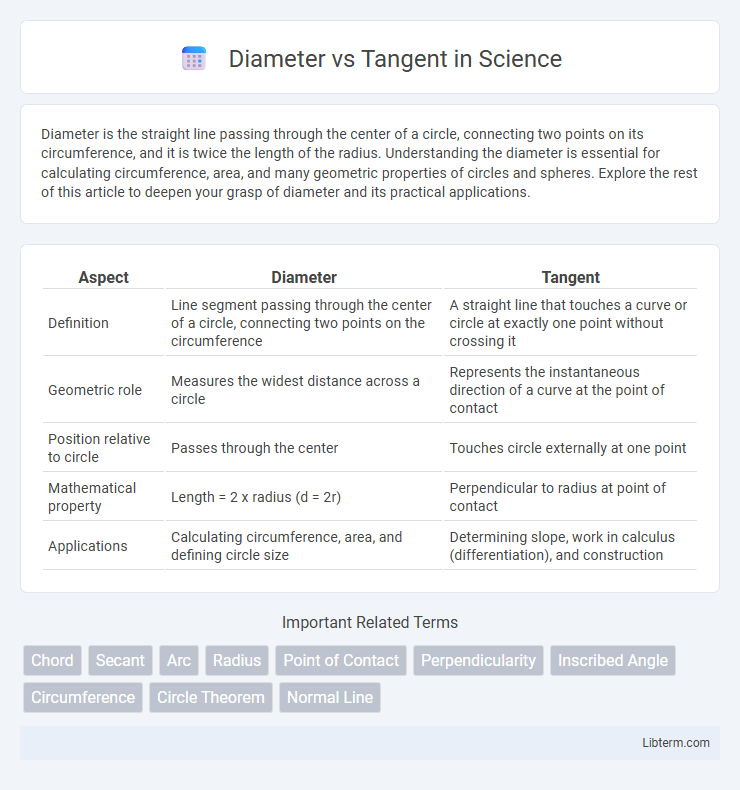
| Aspect | Diameter | Tangent |
|---|---|---|
| Definition | Line segment passing through the center of a circle, connecting two points on the circumference | A straight line that touches a curve or circle at exactly one point without crossing it |
| Geometric role | Measures the widest distance across a circle | Represents the instantaneous direction of a curve at the point of contact |
| Position relative to circle | Passes through the center | Touches circle externally at one point |
| Mathematical property | Length = 2 x radius (d = 2r) | Perpendicular to radius at point of contact |
| Applications | Calculating circumference, area, and defining circle size | Determining slope, work in calculus (differentiation), and construction |
Understanding Diameter and Tangent: Key Definitions
Diameter is a straight line segment passing through the center of a circle connecting two points on its circumference, effectively measuring the circle's longest chord. Tangent is a line that touches the circle at exactly one point, called the point of tangency, without crossing into the circle's interior. Understanding these definitions is fundamental in geometry for solving problems involving circle properties and angles formed by tangents and chords.
The Role of Diameter in Circle Geometry
The diameter is a crucial element in circle geometry, representing the longest chord that passes through the circle's center, effectively dividing the circle into two equal halves. It measures twice the radius, providing a direct calculation for the circle's size and influencing properties like circumference and area through formulas such as C = pd and A = p(d/2)^2. Understanding the diameter's relationship with other elements like the tangent line, which touches the circle at exactly one point, is essential for solving geometric problems involving angles, arcs, and distances within the circle.
What is a Tangent? Properties and Significance
A tangent is a straight line that touches a circle at exactly one point, known as the point of tangency, without crossing the circle's boundary. Key properties include the perpendicularity of the tangent line to the radius drawn to the point of tangency and the fact that it does not intersect the circle at any other point. Tangents are significant in geometry and real-world applications such as engineering and design, where they help in analyzing curves and constructing shapes with precise contact.
Mathematical Relationship: Diameter vs Tangent
The diameter of a circle is a straight line passing through the center, connecting two points on the circle, while a tangent touches the circle at exactly one point without crossing it. The mathematical relationship states that the tangent to a circle is perpendicular to the radius drawn to the point of tangency, and since the diameter is twice the radius, this relationship highlights the diameter's role in defining the length used to establish tangency conditions. In coordinate geometry, the length of the tangent from an external point relates to the diameter through the power of a point theorem, linking these elements in solving circle-related problems.
Visualizing Diameter and Tangent on a Circle
A diameter of a circle is a straight line passing through the center, connecting two points on the circle's circumference, effectively dividing the circle into two equal halves. A tangent is a straight line that touches the circle at exactly one point, called the point of tangency, and it never crosses the circle. Visualizing these, the diameter slices through the circle's center creating a symmetrical division, while the tangent grazes the circle's edge, illustrating the fundamental difference in their interactions with the circle's boundary.
Real-World Applications: Diameter and Tangent Compared
Diameter measures the longest distance passing through the center of a circle, crucial for designing circular components in engineering and manufacturing to ensure precise fit and function. Tangent represents a line that touches a circle at exactly one point without crossing, essential in construction and navigation for determining points of contact and angles of approach. Both concepts play vital roles in fields like architecture, mechanics, and computer graphics where accurate spatial relationships and measurements are required.
Key Differences Between Diameter and Tangent
Diameter is a straight line passing through the center of a circle connecting two points on its circumference, measuring twice the radius, whereas a tangent is a straight line that touches the circle at exactly one point without crossing it. The diameter divides the circle into two equal halves and represents the longest chord, while the tangent is perpendicular to the radius at the point of contact and does not intersect the circle's interior. Understanding these distinctions is crucial in geometry for solving problems related to circle arcs, angles, and lengths.
Common Mistakes: Confusing Diameter with Tangent
Confusing diameter with tangent is a frequent mistake in geometry due to their interactions with a circle. The diameter passes through the center and connects two points on the circle, while a tangent touches the circle at exactly one point without crossing it. Misidentifying these lines can lead to errors in calculating angles, lengths, and solving related problems.
How to Calculate: Diameter and Tangent Formulas
To calculate the diameter of a circle, use the formula \( d = 2r \), where \( r \) is the radius. The tangent length from an external point to the circle can be found using \( t = \sqrt{d^2 - r^2} \), where \( d \) is the distance from the external point to the circle's center. Understanding these formulas is essential for solving geometric problems involving circles and tangents accurately.
Summary Table: Diameter vs Tangent at a Glance
The summary table comparing diameter vs tangent highlights key distinctions in geometry and trigonometry: a diameter passes through the center of a circle and measures twice the radius, while a tangent touches the circle at exactly one point without crossing it. Diameter length is a chord spanning the circle's widest part, whereas a tangent line is perpendicular to the radius at the point of contact. Understanding these differences is essential for solving problems related to circle properties and angle calculations.
Diameter Infographic
 libterm.com
libterm.com