Linked lists are dynamic data structures consisting of nodes, each containing data and a reference to the next node, enabling efficient memory usage and flexible insertion or deletion operations. Unlike arrays, linked lists do not require contiguous memory allocation, making them ideal for applications where data size changes frequently. Explore the rest of the article to understand how linked lists work and their practical implementations in programming.
Table of Comparison
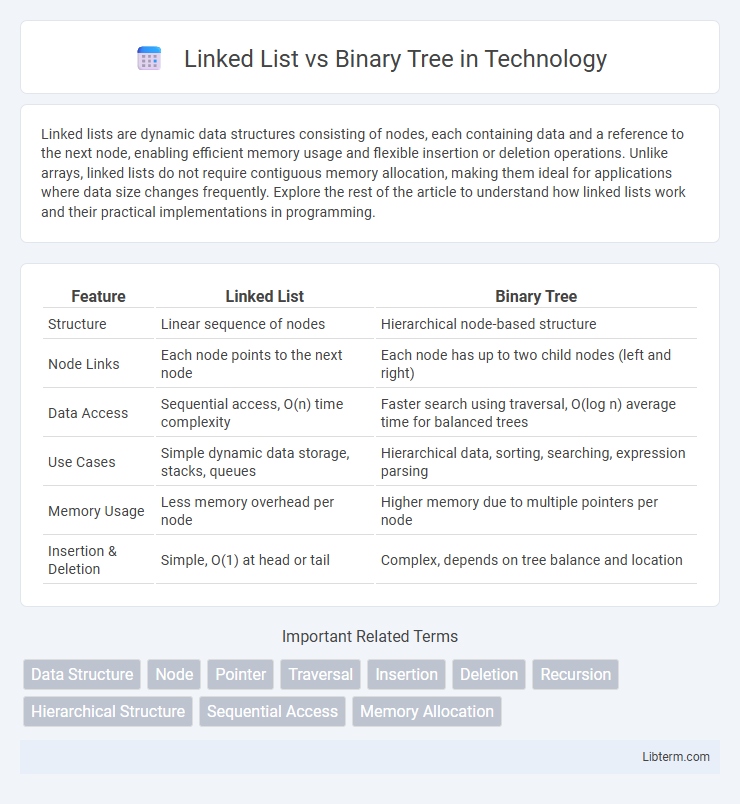
| Feature | Linked List | Binary Tree |
|---|---|---|
| Structure | Linear sequence of nodes | Hierarchical node-based structure |
| Node Links | Each node points to the next node | Each node has up to two child nodes (left and right) |
| Data Access | Sequential access, O(n) time complexity | Faster search using traversal, O(log n) average time for balanced trees |
| Use Cases | Simple dynamic data storage, stacks, queues | Hierarchical data, sorting, searching, expression parsing |
| Memory Usage | Less memory overhead per node | Higher memory due to multiple pointers per node |
| Insertion & Deletion | Simple, O(1) at head or tail | Complex, depends on tree balance and location |
Introduction to Linked Lists and Binary Trees
Linked lists are linear data structures consisting of nodes where each node contains data and a reference to the next node, allowing efficient dynamic memory allocation and easy insertion or deletion of elements. Binary trees are hierarchical data structures with nodes containing data and references to up to two child nodes, commonly referred to as left and right, enabling efficient searching, sorting, and hierarchical organization of data. Both linked lists and binary trees are fundamental structures in computer science used to manage and organize data with distinct advantages depending on the application, such as sequential access in linked lists and logarithmic-time operations in balanced binary trees.
Core Concepts and Definitions
A linked list is a linear data structure consisting of nodes where each node contains data and a reference to the next node, enabling sequential access. A binary tree is a hierarchical data structure where each node has at most two children, referred to as the left and right child, supporting efficient searching and sorting operations. While linked lists provide dynamic memory allocation and ease of insertion or deletion, binary trees facilitate faster lookup, insertion, and deletion through organized node relationships.
Structural Differences
A linked list consists of nodes arranged in a linear sequence where each node points to the next, forming a unidirectional or bidirectional chain. In contrast, a binary tree organizes nodes hierarchically with each node containing references to at most two child nodes, enabling a branching structure. This fundamental structural difference impacts traversal methods and use cases, with linked lists optimized for sequential access and binary trees suited for hierarchical data representation and efficient searching.
Memory Allocation and Usage
Linked lists allocate memory dynamically for each node, storing data and a reference to the next node, resulting in efficient use of memory for sequential data but with overhead for pointer storage. Binary trees also use dynamic memory allocation but require additional pointers per node for left and right children, increasing memory usage compared to linked lists. The hierarchical structure of binary trees enables faster search, insertion, and deletion operations, though at the cost of more complex memory management.
Data Access and Retrieval
Linked lists allow sequential data access where each element points to the next, resulting in O(n) time complexity for retrieval due to linear traversal. Binary trees enable hierarchical data organization that supports faster access times, typically O(log n) for balanced trees, by navigating left or right subtrees to locate elements. Efficient retrieval in binary trees depends on tree balance, while linked lists guarantee simple, albeit slower, sequential access.
Insertion and Deletion Operations
Insertion in a linked list involves updating pointers to add a node at the beginning, end, or any specific position, generally requiring O(1) time for head insertion and O(n) for arbitrary positions. Deletion in a linked list requires adjusting pointers to remove a node, with similar time complexity considerations depending on the node location. In contrast, insertion and deletion in a binary tree depend on the tree type; in a binary search tree, insertion involves locating the correct position maintaining order, often O(log n) on balanced trees, while deletion requires handling node cases such as leaf, one child, or two children, ensuring tree properties are preserved.
Traversal Methods
Linked lists utilize a linear traversal method, where each node is visited sequentially starting from the head until the end is reached, making operations like insertion and deletion straightforward. Binary trees employ various traversal techniques such as in-order, pre-order, and post-order, which enable visiting nodes in specific hierarchical sequences to support diverse applications like expression evaluation and sorted data retrieval. Tree traversals often utilize recursion or stacks, whereas linked list traversal is inherently iterative, reflecting fundamental structural differences between linear and hierarchical data storage.
Use Cases and Applications
Linked lists excel in dynamic memory allocation and efficient insertion or deletion of elements in applications like implementing stacks, queues, and adjacency lists for graphs. Binary trees, particularly binary search trees, are ideal for hierarchical data representation, enabling fast searching, sorting, and priority-based access in scenarios such as database indexing, file system organization, and expression parsing. Use cases for binary trees extend to balanced trees like AVL and red-black trees, optimizing search performance in real-time systems and complex data structures.
Performance and Efficiency Comparison
Linked lists offer efficient sequential access with O(n) time complexity for search operations, while binary trees, particularly balanced ones, provide faster O(log n) search, insertion, and deletion due to hierarchical node structure. Memory usage in linked lists is lower per node, as they typically store only data and a pointer, whereas binary trees maintain additional pointers for multiple child nodes, increasing overhead. In use cases requiring sorted data or frequent search operations, balanced binary trees deliver superior performance and efficiency compared to linked lists.
Choosing Between Linked List and Binary Tree
Choosing between a linked list and a binary tree depends on the data structure's intended use and performance requirements. Linked lists are ideal for sequential access with dynamic memory allocation and easy insertion or deletion, while binary trees offer efficient hierarchical data representation and faster search, insert, and delete operations through sorting. For scenarios requiring quick lookups and ordered traversal, balanced binary trees like AVL or Red-Black trees outperform linked lists in time complexity.
Linked List Infographic
 libterm.com
libterm.com