Heap is a specialized tree-based data structure that satisfies the heap property, where each parent node is either greater than or equal to (max-heap) or less than or equal to (min-heap) its child nodes. It is widely used to implement priority queues and efficiently retrieve the highest or lowest priority element. Explore the rest of the article to understand how heaps optimize your data processing tasks.
Table of Comparison
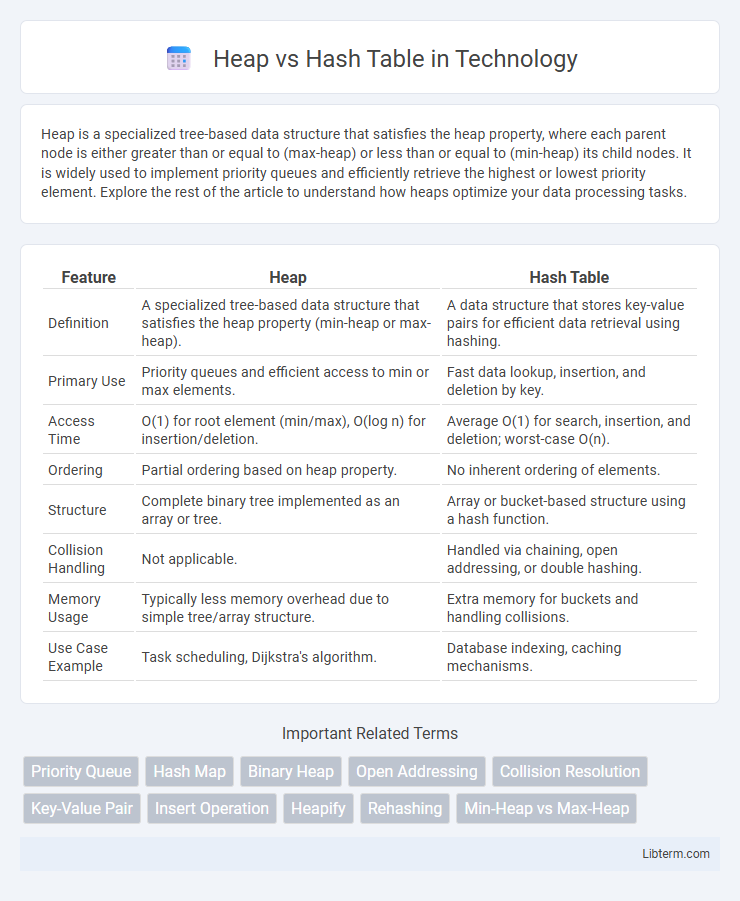
| Feature | Heap | Hash Table |
|---|---|---|
| Definition | A specialized tree-based data structure that satisfies the heap property (min-heap or max-heap). | A data structure that stores key-value pairs for efficient data retrieval using hashing. |
| Primary Use | Priority queues and efficient access to min or max elements. | Fast data lookup, insertion, and deletion by key. |
| Access Time | O(1) for root element (min/max), O(log n) for insertion/deletion. | Average O(1) for search, insertion, and deletion; worst-case O(n). |
| Ordering | Partial ordering based on heap property. | No inherent ordering of elements. |
| Structure | Complete binary tree implemented as an array or tree. | Array or bucket-based structure using a hash function. |
| Collision Handling | Not applicable. | Handled via chaining, open addressing, or double hashing. |
| Memory Usage | Typically less memory overhead due to simple tree/array structure. | Extra memory for buckets and handling collisions. |
| Use Case Example | Task scheduling, Dijkstra's algorithm. | Database indexing, caching mechanisms. |
Introduction to Heap and Hash Table
A heap is a specialized tree-based data structure that satisfies the heap property, where the key at the root must be either the minimum or maximum among all keys in the tree, making it ideal for priority queue implementations. A hash table uses a hash function to map keys to specific indices in an array, enabling efficient average-time complexity for search, insert, and delete operations. Both structures optimize data retrieval, with heaps focusing on order and priority, while hash tables emphasize fast access via key-value pairs.
Definitions and Core Concepts
A heap is a specialized tree-based data structure that satisfies the heap property, where each parent node is either greater than or equal to (max-heap) or less than or equal to (min-heap) its child nodes, enabling efficient priority queue operations. A hash table is a data structure that maps keys to values using a hash function, allowing average-case constant time complexity for insertions, deletions, and lookups. While heaps prioritize maintaining a partial order for quick access to the maximum or minimum element, hash tables optimize direct key-based retrieval.
Data Structure Overview: Heap
A heap is a specialized tree-based data structure that satisfies the heap property, where each parent node is ordered with respect to its children, commonly used to implement priority queues. It is typically represented as a complete binary tree, enabling efficient insertion, deletion, and access to the minimum or maximum element in O(log n) time. Unlike hash tables that provide average O(1) time complexity for lookups by hashing keys, heaps prioritize maintaining a partial order useful for sorting and priority management tasks.
Data Structure Overview: Hash Table
A hash table is a data structure that stores key-value pairs and uses a hash function to compute an index into an array of buckets or slots, enabling efficient data retrieval. It offers average-case time complexity of O(1) for search, insertion, and deletion operations due to direct addressing. Hash tables handle collisions through methods like chaining or open addressing, maintaining performance in varied data scenarios.
Key Differences Between Heap and Hash Table
Heap is a specialized tree-based data structure primarily used for efficient priority queue operations, maintaining a partial order where the parent node is either greater or smaller than its child nodes. Hash table is an associative array data structure providing average-case constant-time complexity for search, insert, and delete operations by using a hash function to map keys to bucket indices. Unlike heaps that focus on order and priority, hash tables emphasize fast access and retrieval of values based on unique keys without inherent sorting.
Use Cases of Heap
Heaps are ideal for priority queue implementations where quick access to the highest or lowest priority element is required, such as task scheduling, Dijkstra's shortest path algorithm, and event simulation systems. Unlike hash tables, which excel in fast key-value lookups, heaps maintain a partially ordered structure that supports efficient insertion and extraction of the minimum or maximum element. Use cases benefiting from dynamic order statistics and priority management rely heavily on heap data structures for optimal performance.
Use Cases of Hash Table
Hash tables excel in use cases requiring rapid data retrieval, such as implementing associative arrays, caches, and database indexing, where average time complexity for lookups is O(1). They efficiently handle dynamic sets of key-value pairs, making them ideal for symbol tables in compilers, frequency counting in data analysis, and managing unique elements in hash sets. Hash tables are fundamental in applications demanding quick membership tests, such as routing tables in networking and session management in web development.
Performance Comparison: Time and Space Complexity
Heap structures provide O(log n) time complexity for insertion and deletion operations, making them highly efficient for priority queue tasks, while hash tables offer average O(1) time complexity for search, insert, and delete operations, optimizing key-value access. However, hash tables typically require more space than heaps due to maintaining an underlying array and handling collisions with techniques like chaining or open addressing. Memory usage in heaps is more compact, storing elements in a tree structure without extra space overhead, leading to efficient utilization in scenarios with limited memory.
Advantages and Disadvantages
Heap structures excel in priority queue operations with efficient O(log n) insertion and extraction of the minimum or maximum element, providing excellent performance for dynamic datasets. However, heaps lack efficient search capabilities, making them unsuitable for quick element lookup compared to hash tables. Hash tables offer average O(1) time complexity for insertions, deletions, and lookups due to direct addressing, but they require extra memory for storage and can experience performance degradation from collisions and poor hash functions.
Choosing the Right Structure: When to Use Heap vs Hash Table
A heap is ideal for priority-based operations where maintaining a dynamic set of elements with quick access to the minimum or maximum value is crucial, such as in scheduling algorithms or implementing priority queues. A hash table excels in scenarios requiring fast average-time complexity for insertion, deletion, and search operations, making it suitable for dictionary implementations or caching mechanisms. Choosing between a heap and a hash table depends on whether the primary need is ordered element retrieval or efficient key-based access.
Heap Infographic
 libterm.com
libterm.com