Reed-Solomon codes are powerful error-correcting codes widely used in digital communications and data storage to detect and correct multiple symbol errors. Their robust capability to recover lost or corrupted information makes them essential in applications such as CDs, DVDs, QR codes, and satellite transmissions. Explore the rest of this article to understand how Reed-Solomon codes enhance your data reliability and integrity.
Table of Comparison
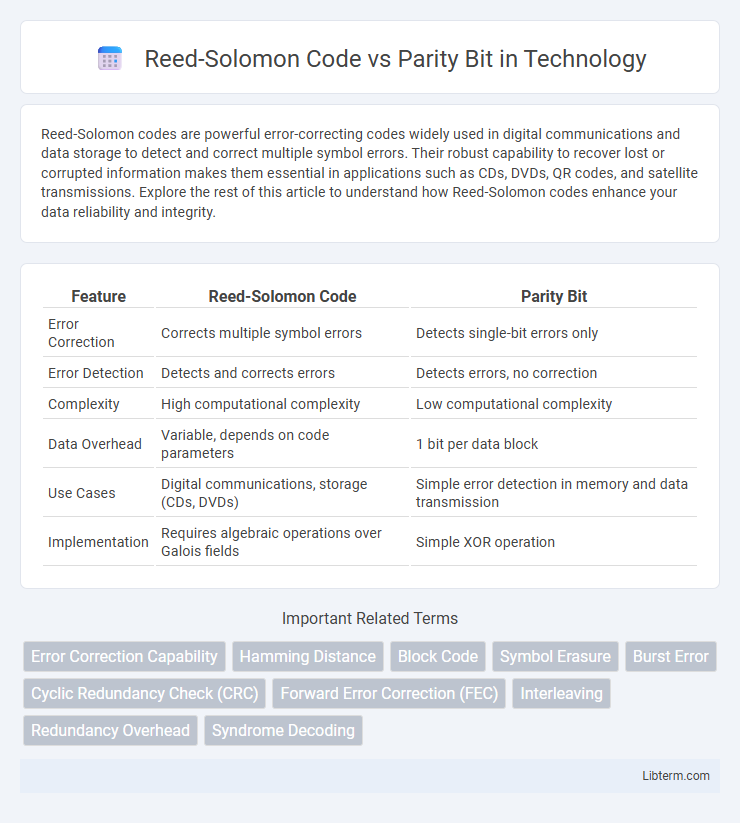
| Feature | Reed-Solomon Code | Parity Bit |
|---|---|---|
| Error Correction | Corrects multiple symbol errors | Detects single-bit errors only |
| Error Detection | Detects and corrects errors | Detects errors, no correction |
| Complexity | High computational complexity | Low computational complexity |
| Data Overhead | Variable, depends on code parameters | 1 bit per data block |
| Use Cases | Digital communications, storage (CDs, DVDs) | Simple error detection in memory and data transmission |
| Implementation | Requires algebraic operations over Galois fields | Simple XOR operation |
Introduction to Error Detection and Correction
Reed-Solomon codes provide robust error detection and correction by encoding data into fixed-length blocks, allowing for the correction of multiple symbol errors within each block. Parity bit methods offer simpler error detection by adding a single bit to data sequences, typically identifying only single-bit errors without correction capabilities. These coding techniques are fundamental in digital communication and storage, with Reed-Solomon favored in applications requiring high reliability and parity bits used for basic error monitoring.
Overview of Reed-Solomon Codes
Reed-Solomon codes are a class of powerful error-correcting codes used extensively in digital communications and storage, capable of correcting multiple symbol errors in data blocks. Unlike simple parity bits, which provide minimal error detection by adding a single bit to indicate odd or even parity, Reed-Solomon codes use polynomial algebra over finite fields to encode data with redundant symbols. This robust coding technique enhances data integrity in applications such as satellite communications, QR codes, and RAID systems by enabling precise error correction and data recovery.
Understanding Parity Bits
Parity bits serve as a basic form of error detection by adding a single bit to data, indicating whether the number of 1s is even or odd, which helps identify single-bit errors. Reed-Solomon codes extend this concept by using multiple parity symbols spread across data blocks to detect and correct multiple errors, making them suitable for complex error-prone environments like digital storage and communication systems. Understanding parity bits lays the foundation for grasping more advanced error correction techniques such as Reed-Solomon encoding.
Key Differences Between Reed-Solomon Codes and Parity Bits
Reed-Solomon codes provide robust error correction by encoding data into multiple symbols, allowing recovery from multiple symbol errors in data transmission or storage. Parity bits offer basic error detection by adding a single bit that indicates whether the number of set bits is even or odd, but cannot correct errors on their own. The key differences lie in Reed-Solomon's ability to correct multiple errors and handle burst errors, while parity bits only detect single-bit errors without correction capability.
Error Correction Capabilities: Reed-Solomon vs Parity Bit
Reed-Solomon codes provide robust error correction by detecting and correcting multiple symbol errors within data blocks, making them highly effective in applications like digital communications and storage media. Parity bits offer only basic error detection, typically identifying single-bit errors without the capability to correct them, resulting in limited reliability for error correction. The superior error correction capabilities of Reed-Solomon codes enable recovery from burst errors, which parity bits cannot handle, significantly enhancing data integrity in error-prone environments.
Typical Applications of Reed-Solomon Code
Reed-Solomon codes are widely used in digital communications and storage systems, including CDs, DVDs, QR codes, and satellite communications, due to their strong error correction capabilities that can recover multiple symbol errors. Unlike simple parity bits, which only detect single-bit errors, Reed-Solomon codes correct burst errors and erasures, making them essential for applications requiring high data integrity in noisy environments. Their implementation in deep-space communication and RAID storage systems highlights their critical role in ensuring reliable data transmission and long-term data preservation.
Common Uses of Parity Bit Systems
Parity bit systems are commonly employed in simple error detection tasks such as data transmission in serial communication protocols, memory storage error checking like in DRAM modules, and basic network communications including Ethernet frames. These systems use a single parity bit appended to data blocks to detect single-bit errors efficiently, making them suitable for environments where error rates are low and correction is not critical. Reed-Solomon codes, by contrast, are favored in complex applications such as digital television broadcasting, QR codes, and RAID storage systems because they provide robust error correction capabilities for multiple symbol errors.
Performance and Efficiency Comparison
Reed-Solomon codes provide superior error correction capabilities compared to simple parity bits, enabling the recovery of multiple symbol errors within a data block, which significantly enhances data reliability in noisy communication channels. While parity bits offer minimal overhead and fast encoding/decoding suitable for detecting single-bit errors, their error correction capacity is limited, making them less efficient in scenarios with higher error rates. Reed-Solomon codes, though computationally more intensive, deliver higher performance in environments demanding robust error correction, such as digital television and data storage systems.
Implementation Complexity: Parity Bit vs Reed-Solomon
Parity bit implementation is straightforward, requiring minimal hardware or software resources to detect single-bit errors using a single additional bit. Reed-Solomon codes involve complex mathematical operations over finite fields, necessitating advanced encoding and decoding algorithms, often implemented with specialized hardware or optimized software libraries. The implementation complexity of Reed-Solomon codes significantly exceeds parity bit schemes but offers superior error correction capabilities for burst errors and multi-bit error patterns.
Choosing the Right Error Correction Method
Reed-Solomon codes provide robust error correction by correcting multiple symbol errors, making them ideal for applications such as digital television and data storage where data integrity is critical. Parity bits offer simpler, single-bit error detection and are suitable for low-complexity systems with minimal error correction needs like basic memory checks. Choosing the right error correction method depends on the error environment, system complexity, and data reliability requirements.
Reed-Solomon Code Infographic
 libterm.com
libterm.com